Условие задачи:
Моторная лодка проходит расстояние между двумя пунктами A и B по течению реки за 3 ч, а плот — за 12 ч. Сколько времени затратит моторная лодка на обратный путь?
Задача №1.7.15 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(t_1=3\) ч, \(t_0=12\) ч, \(t_2-?\)
Решение задачи:
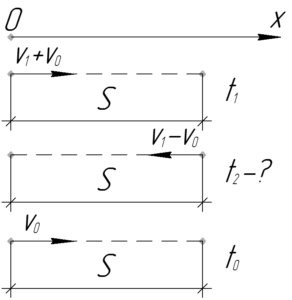 И лодка, и плот проходят одно и то же расстояние \(S\), только с разными скоростями. Плот может плыть только по течению реки со скоростью течения \(\upsilon_0\). Моторная лодка движется по течению со скоростью \((\upsilon_1+\upsilon_0)\), а против течения — \((\upsilon_1-\upsilon_0)\), где \(\upsilon_1\) — скорость лодки в стоячей воде. Исходя из этого, запишем следующую систему:
И лодка, и плот проходят одно и то же расстояние \(S\), только с разными скоростями. Плот может плыть только по течению реки со скоростью течения \(\upsilon_0\). Моторная лодка движется по течению со скоростью \((\upsilon_1+\upsilon_0)\), а против течения — \((\upsilon_1-\upsilon_0)\), где \(\upsilon_1\) — скорость лодки в стоячей воде. Исходя из этого, запишем следующую систему:
\[\left\{ \begin{gathered}
S = \left( {{\upsilon _1} + {\upsilon _0}} \right){t_1}\;\;\;\;(2) \hfill \\
S = \left( {{\upsilon _1} — {\upsilon _0}} \right){t_2}\;\;\;\;(2) \hfill \\
S = {\upsilon _0}{t_0}\;\;\;\;(3) \hfill \\
\end{gathered} \right.\]
Левые части уравнений (1) и (3) равны, а значит равны и правые.
\[\left( {{\upsilon _1} + {\upsilon _0}} \right){t_1} = {\upsilon _0}{t_0}\]
Найдем отношение \(\frac{\upsilon_1}{\upsilon_0}\).
\[\frac{{{\upsilon _1} + {\upsilon _0}}}{{{\upsilon _0}}} = \frac{{{t_0}}}{{{t_1}}}\]
\[\frac{{{\upsilon _1}}}{{{\upsilon _0}}} + 1 = \frac{{{t_0}}}{{{t_1}}}\]
\[\frac{{{\upsilon _1}}}{{{\upsilon _0}}} = \frac{{{t_0}}}{{{t_1}}} — 1\]
Отлично, теперь поработаем над выражением (2) и (3). Аналогично:
\[\left( {{\upsilon _1} — {\upsilon _0}} \right){t_2} = {\upsilon _0}{t_0}\]
\[{t_2} = {t_0}\frac{{{\upsilon _0}}}{{{\upsilon _1} — {\upsilon _0}}}\]
И числитель, и знаменатель дроби в правой части равенства поделим на \(\upsilon_0\).
\[{t_2} = {t_0}\frac{1}{{\frac{{{\upsilon _1}}}{{{\upsilon _0}}} — 1}}\]
Подставим найденное нами отношение скоростей.
\[{t_2} = {t_0}\frac{1}{{\frac{{{t_0}}}{{{t_1}}} — 1 — 1}}\]
\[{t_2} = {t_0}\frac{1}{{\frac{{{t_0}}}{{{t_1}}} — 2}}\]
В итоге:
\[{t_2} = \frac{{{t_0}{t_1}}}{{{t_0} — 2{t_1}}}\]
Сосчитаем ответ:
\[{t_2} = \frac{{12 \cdot 3}}{{12 — 2 \cdot 3}} = 6\; ч\]
Ответ: 6 ч.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.7.14 Когда нет ветра, капли дождя оставляют на окне равномерно движущегося вагона
1.7.16 Пассажир едет в поезде, скорость которого 80 км/ч. Навстречу этому поезду
1.7.17 Пловец переплывает реку по прямой, перпендикулярной берегу. Определить

Темпераментные лучшие феи в Барнауле, сладкие и ухоженные, они такие изобретательные и стройные, что любой захочет их. Не упусти свой шанс. Бесподобные леди встречаются с приятными, чистоплотными мужчинами, лучшие феи в Барнауле, для жаркого времяпровождения. В уютной квартире вас встретить проститутка и вы воплотите все ваши желания в жизнь.
 icodepro.ru
icodepro.ru
вот оно как, всегда думал что плот это нечто с парусом
Уважаемый автор, откуда у вас в конечной формуле перед двойкой появилось t1, если в предыдущей формуле вы перекинули его в числитель?
Я избавился от дроби в знаменателе, умножив и числитель, и знаменатель на \(t_1\).
\[{t_2} = {t_0}\frac{1}{{\frac{{{t_0}}}{{{t_1}}} — 2}}\]
\[{t_2} = \frac{{{t_0}{t_1}}}{{{t_0} — 2{t_1}}}\]
В данном случае нельзя \(t_1\) перекинуть в числитель, поскольку в знаменателе выражение \(\left( {\frac{{{t_0}}}{{{t_1}}} — 2} \right)\), а не \({\frac{{{t_0}}}{{{t_1}}}}\).