Пассажир едет в поезде, скорость которого 80 км/ч. Навстречу этому поезду

Условие задачи:

Пассажир едет в поезде, скорость которого 80 км/ч. Навстречу этому поезду едет товарный поезд длиной 1 км со скоростью 40 км/ч. Сколько времени пассажир будет видеть товарный поезд?

Задача №1.7.16 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\upsilon_1=80\) км/ч, \(L_2=1\) км, \(\upsilon_2=40\) км/ч, \(t-?\)

Решение задачи:

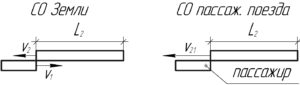Чтобы оказаться на месте пассажира, перейдем в систему отсчета, связанную с поездом, в котором он едет. Понятно, что в этой СО модуль скорости товарного поезда равен сумме скоростей поездов относительно земли. Почему получилось так? Дело в том, чтобы перейти в СО первого поезда, нужно к вектору скорости товарного поезда относительно Земли \(\overrightarrow {{\upsilon _2}}\) прибавить вектор, равный по величине и противоположный по направлению вектору скорости пассажирского, то есть \(– \overrightarrow {{\upsilon _1}}\).

\[{\upsilon _{21}} = {\upsilon _1} + {\upsilon _2}\]

Так как “товарняк” движется равномерно, что легко найти время, спрашиваемое в задании.

\[{L_2} = {\upsilon _{21}}t \Rightarrow t = \frac{{{L_2}}}{{{\upsilon _{21}}}}\]

\[t = \frac{{{L_2}}}{{{\upsilon _1} + {\upsilon _2}}}\]

Хочу заметить, что за это время товарный поезд пройдет только мимо пассажира. Если было бы нужно найти сколько времени поезда движутся мимо друг друга, то было бы нужно сумму длин поездов делить на ту же относительную скорость.

Переводить исходные данные в систему СИ не будем, в этом случае мы изначально получим ответ в часах, поскольку расстояние дано в километрах, а скорость – в километрах в час.

\[t = \frac{1}{{80 + 40}} = \frac{1}{{120}}\; ч\]

Переведем время из часов в секунды, для этого умножим дробь на 3600 (это количество секунд в часах).

\[\frac{1}{{120}}\; ч = \frac{{1 \cdot 3600}}{{120}}\; с = 30\; с\]

Ответ: 30 с.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

1.7.15 Моторная лодка проходит расстояние между двумя пунктами A и B по течению реки
1.7.17 Пловец переплывает реку по прямой, перпендикулярной берегу. Определить
1.7.18 Пассажирский поезд идет со скоростью 72 км/ч. По соседнему пути движется