При равноускоренном движении тело проходит за четвертую секунду 16 м. Определить

Условие задачи:

При равноускоренном движении тело проходит за четвертую секунду 16 м. Определить перемещение тела за седьмую секунду. Начальная скорость тела 2 м/с.

Задача №1.4.24 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(S_4=16\) м, \(\upsilon_0=2\) м/с, \(S_7-?\)

Решение задачи:

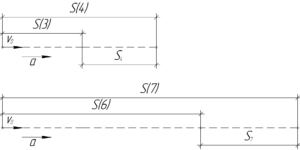Путь за четвертую секунду \(S_4\) есть разница между путем за четыре \(S(4)\) и путем за три секунды \(S(3)\).

\[{S_4} = S(4) – S(3)\;\;\;\;(1)\]

Так как движение тела равноускоренное, то запишем стандартные формулы для определения \(S(4)\) и \(S(3)\), введя время \(t_4\) и \(t_3\), равные 4 и 3 секунды соответственно. В ходе дальнейшего решения остальные обозначения времени следует понимать аналогично.

\[S(4) = {\upsilon _0}{t_4} + \frac{{at_4^2}}{2}\;\;\;\;(2)\]

\[S(3) = {\upsilon _0}{t_3} + \frac{{at_3^2}}{2}\;\;\;\;(3)\]

Подставим формулы (2) и (3) в (1).

\[{S_4} = {\upsilon _0}{t_4} + \frac{{at_4^2}}{2} – {\upsilon _0}{t_3} – \frac{{at_3^2}}{2}\]

\[{S_4} = {\upsilon _0}\left( {{t_4} – {t_3}} \right) + \frac{{a\left( {t_4^2 – t_3^2} \right)}}{2}\]

Выразим из последней формулы неизвестное ускорение \(a\).

\[a = \frac{{2{S_4} – 2{\upsilon _0}\left( {{t_4} – {t_3}} \right)}}{{\left( {t_4^2 – t_3^2} \right)}}\]

Аналогично распишем выражение для нахождения пути за седьмую секунду \(S_7\).

\[{S_7} = S(7) – S(6)\]

\[S(7) = {\upsilon _0}{t_7} + \frac{{at_7^2}}{2}\]

\[S(6) = {\upsilon _0}{t_6} + \frac{{at_6^2}}{2}\]

Значит:

\[{S_7} = {\upsilon _0}\left( {{t_7} – {t_6}} \right) + \frac{{a\left( {t_7^2 – t_6^2} \right)}}{2}\]

Подставим в последнюю формулу выражение для ускорения \(a\). В итоге получим окончательную формулу.

\[{S_7} = {\upsilon _0}\left( {{t_7} – {t_6}} \right) + \frac{{\left( {{S_4} – {\upsilon _0}\left( {{t_4} – {t_3}} \right)} \right)\left( {t_7^2 – t_6^2} \right)}}{{\left( {t_4^2 – t_3^2} \right)}}\]

Теперь сосчитаем ответ численно.

\[{S_7} = 2\left( {7 – 6} \right) + \frac{{\left( {16 – 2\left( {4 – 3} \right)} \right)\left( {{7^2} – {6^2}} \right)}}{{\left( {{4^2} – {3^2}} \right)}} = 28\; м \]

Конечно, можно было не вводить время буквенно (\(t_4\), \(t_3\) и т.д.), а подставлять их численно, тогда конечная формула была бы короче, но не совпадала бы по размерности. Лично мне нравится именно такой вариант решения.

Ответ: 28 м.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

1.4.23 Определите время равноускоренного движения снаряда в стволе длиной 3 м
1.4.25 С вертолета, находящегося на высоте 500 м, упал камень. Через какое время
1.4.26 С какой высоты падало тело, если за последние 2 с прошло путь 60 м?