icodepro.ruУсловие задачи:
Снаряд вылетает из орудия со скоростью 1000 м/с под углом 60° к горизонту. Найдите кратчайшее расстояние от орудия до точки разрыва снаряда, если в момент разрыва вектор его скорости составлял с горизонтом угол 45°. Сопротивлением воздуха пренебречь.
Задача №1.6.10 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(v_0=1000\) м/с, \(\alpha=60^\circ\), \(\beta=45^\circ\), \(S-?\)
Решение задачи:
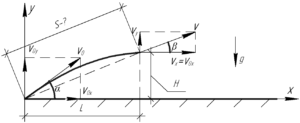Рисунок к решению приведенной задачи изображен справа.
Прочитав условие задачи, заметим сей факт, что в момент разрыва вектор его скорости составлял с горизонтом угол 45°. Это означает, что в этот момент, составляющие вектора скорости (т.е. его проекции на ось \(x\) и \(y\)) равны, поскольку в прямоугольном треугольнике с углом 45° катеты равны.
Запишем уравнения скорости в проекциях на оси \(x\) и \(y\):
\[\left\{ \begin{gathered}
ox:{v_x} = {v_0}\cos \alpha \,\,\,\,\,\,\,\,\,\,\,\,(1) \hfill \\
oy:{v_y} = {v_0}\sin \alpha – gt\,\,(2) \hfill \\
\end{gathered} \right.\]
Руководствуясь вышесказанным, запишем условие равенства составляющих в момент разрыва снаряда.
\[{v_0}\sin \alpha – gt = {v_0}\cos \alpha \]
Отсюда найдем время полета снаряда до момента его разрыва:
\[t = \frac{{{v_0}\left( {\sin \alpha – \cos \alpha } \right)}}{g}\]
Подставим все известные величины в системе измерения СИ и найдем численно время. Решение задачи в общем виде нецелесообразно, т.к. конечная формула будет огромная.
\[t = \frac{{1000\left( {\sin 60^\circ – \cos 60^\circ } \right)}}{{10}} = 36,60\; с.\]
В задаче необходимо найти кратчайшее расстояние от орудия до точки разрыва снаряда, для этого взглянем на рисунок и увидим, что его можно найти из теоремы Пифагора:
\[S = \sqrt {{L^2} + {H^2}} \]
Запишем уравнения движения в проекциях на оси \(x\) и \(y\):
\[\left\{ \begin{gathered}
ox:x = {v_0}\cos \alpha \cdot t\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(3) \hfill \\
oy:y = {v_0}\sin \alpha \cdot t – \frac{{g{t^2}}}{2}\,\,\,(4) \hfill \\
\end{gathered} \right.\]
Подставим все известные и найдем численно расстояния:
\[L = {v_0}\cos \alpha \cdot t\]
\[L = 1000 \cdot \cos 60^\circ \cdot 36,60 = 18300\; м.\]
\[H = {v_0}\sin \alpha \cdot t – \frac{{g{t^2}}}{2}\]
\[H = 1000 \cdot \sin 60^\circ \cdot 36,60 – \frac{{10 \cdot {{36,60}^2}}}{2} = 25000\; м.\]
В итоге:
\[S = \sqrt {{{18300}^2} + {{25000}^2}} \approx 31000\; м.\]
Ответ: 31000 м.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Если Вам понравилась задача и ее решение, то Вы можете поделитесь ею с друзьями с помощью этих кнопок.
Смотрите также задачи:
1.6.9 Пуля вылетает из ствола под углом 45 градусов к горизонту
1.6.11 Тело бросили под углом 60 градусов к горизонту со скоростью 10 м/с
1.6.12 Тело брошено с начальной скоростью 40 м/с под углом 30 градусов
В условии сказано сопротивлением воздуха пренебречь, а меня интересует наоборот, когда сопротивление воздуха учитывается, как в таком случае решается задача? И каким будет алгоритм решения таких задач, когда учитывается сопротивление воздуха (формулы, пояснения)?
Попробую объяснить кратко. Сила сопротивления воздуха в зависимости от скорости движения тела (если мне не изменяет память) описывается разными формулами, например одна из них: \[F = k{\upsilon ^2}\]Здесь \(k\) – некоторый коэффициент сопротивления. Записывается второй закон Ньютона для данного тела, например, для тела, движущегося под действием силы \(F\) вдоль оси \(x\), в векторном виде эта формула будет иметь вид: \[\overrightarrow F + k{\overrightarrow \upsilon ^2} = m\overrightarrow a \]В проекции на ось \(x\) это уравнение запишется так:\[F – k{\upsilon ^2} = ma\]Мы получили дифференциальное уравнение, методы решения таких уравнений рассматриваются уже в ВУЗе. Замечу, что мы рассмотрели самое простое движение с сопротивлением вдоль одной оси. Сложное движение по двум осям (как в этой задаче) с сопротивлением скорее всего вообще не будет иметь аналитического решения (т.е. невозможно получить одной общей формулы решения) и её придется решать численно.