Свободно падающее без начальной скорости тело пролетело мимо точки A

Условие задачи:

Свободно падающее без начальной скорости тело пролетело мимо точки A со скоростью \(\upsilon_A\). С какой скоростью оно пролетит мимо точки B, находящейся на расстоянии \(h\) ниже точки A?

Задача №1.4.49 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\upsilon_A\), \(h\), \(\upsilon_B-?\)

Решение задачи:

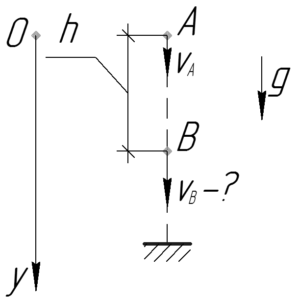Для того чтобы ответить на вопрос задачи, воспользуемся следующей формулой:

\[\upsilon _B^2 – \upsilon _A^2 = 2gh\]

По сути эта формула является преобразованным законом сохранения энергии.

Как записать такую формулу? Просто записать разность квадратов конечной и начальной скорости слева и удвоенное произведение модуля ускорения и пути справа, причем если тело замедлялось, то в правой части будет фигурировать знак “минус”.

Выразим искомую скорость тела в точке B:

\[{\upsilon _B} = \sqrt {\upsilon _A^2 + 2gh} \]

Как вы видите, это очень простая задача на знание лишь одной формулы.

Ответ: \({\upsilon _B} = \sqrt {\upsilon _A^2 + 2gh}\)

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

1.4.48 Цепочка шаров висит над поверхностью стола: первый шар – на высоте 1 м, второй
1.4.50 За последнюю секунду свободно падающее без начальной скорости тело
1.4.51 Мяч, брошенный вертикально вверх, упал на землю через 3 с. Чему равна величина