icodepro.ruУсловие задачи:
Тело, брошенное вертикально вверх, за третью секунду прошло 5 м. Определить начальную скорость тела.
Задача №1.4.22 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(S_3=5\) м, \(\upsilon_0-?\)
Решение задачи:
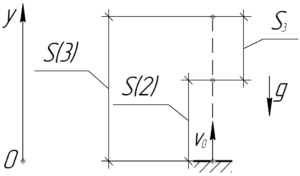Важно! Не путайте “путь за третью секунду” и “путь за три секунды” – это принципиально разные понятия. Если второе показывает сколько тело прошло за три секунды от начала движения, то второе – сколько тело прошло именно за третью. Например, в данном случае путь за третью секунду \(S_3\) – это разность между путем за три секунды \(S\left( 3 \right)\) и путем за две секунды \(S\left( 2 \right)\) (на изображении к задаче видно наглядно в чем разница). Замечу, что нет пути за нулевую секунду, отсчет ведется с единицы.
\[{S_3} = S\left( 3 \right) – S\left( 2 \right)\]
Запишем уравнение движения вдоль оси \(y\):
\[y = \upsilon_0 t – \frac{{g{t^2}}}{2}\]
Будем считать, что тело не поменяет направление своего движения за третью секунду, иначе задача бы усложнилась. В этом случае координата \(y\) показывает пройденный за время \(t\) путь. Тогда:
\[S\left( 3 \right) = \upsilon_0 \cdot {t_3} – \frac{{gt_3^2}}{2}\]
\[S\left( 2 \right) = \upsilon_0 \cdot {t_2} – \frac{{gt_2^2}}{2}\]
В этих формулах \(t_2\) и \(t_3\) – это время 2 и 3 секунды соответственно. В итоге:
\[{S_3} = \upsilon_0 \cdot {t_3} – \frac{{gt_3^2}}{2} – \upsilon_0 \cdot {t_2} + \frac{{gt_2^2}}{2}\]
\[{S_3} = \upsilon_0 \left( {{t_3} – {t_2}} \right) – \frac{g}{2}\left( {t_3^2 – t_2^2} \right)\]
\[\upsilon_0 = \frac{{{S_3} + \frac{g}{2}\left( {t_3^2 – t_2^2} \right)}}{{\left( {{t_3} – {t_2}} \right)}}\]
\[\upsilon_0 = \frac{{2{S_3} + g\left( {t_3^2 – t_2^2} \right)}}{{2\left( {{t_3} – {t_2}} \right)}}\]
Сосчитаем ответ численно:
\[\upsilon_0 = \frac{{2 \cdot 5 + 10\left( {{3^2} – {2^2}} \right)}}{{2\left( {3 – 2} \right)}} = 30\; м/с\]
Кстати, наше предположение, что тело за третью секунду не меняет своего направления, оказалось верным.
Ответ: 30 м/с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.4.21 Тело бросают вертикально вверх. Наблюдатель замечает промежуток времени
1.4.23 Определите время равноускоренного движения снаряда в стволе длиной 3 м
1.4.24 При равноускоренном движении тело проходит за четвертую секунду 16 м. Определить
Данная задача – крайняя: при t = 3 c тело достигает max высоты…
Как будите решать задачу:
t1 = 1 c, t2 = 4 c, S = 25 м, V0 = ?
!!!
А если бы тело поменяло бы направление? ТО считать так же?
Интересный вопрос, заставил меня хорошо подумать.
Каким образом можно узнать, что тело поменяло свое направление? Дело в том, что за одну секунду вертикально брошенное тело проходит не менее 5 м. Причем, если тело прошло ровно 5 м, то либо это последняя секунду движения вверх, либо это первая секунда движения вниз.
Сразу становится понятно, что мы потеряли еще одно решение представленной задачи – при начальной скорости 20 м/с тело за третью секунду также пройдет 5 м.
Так вот, возвращаясь к Вашу вопросу: если тело вертикально брошенное тело за n-ную секунду прошло менее 5 м, значит за эту n-ную секунду тело поменяло направление своего движения. В этом случае Вам нужно начертить график функции \(\upsilon \left( t \right)\) так, чтобы в n-ную секунду график пересек ось \(t\). Далее Вам нужно воспользоваться тем, что площадь под графиком скорости есть пройденный путь.