Тело брошено с начальной скоростью 40 м/с под углом 30 градусов

Условие задачи:

Тело брошено с начальной скоростью 40 м/с под углом 30° к горизонту. Через какое минимальное время от начала движения тело поднялось на половину максимальной высоты?

Задача №1.6.12 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(v_0=40\) м/с, \(\alpha=30^\circ\), \(h = \frac{H}{2}\), \(t_1-?\)

Решение задачи:

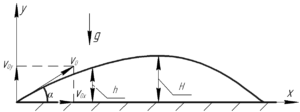Чтобы решить любую задачу, сперва необходимо сделать к ней рисунок. Так как в условии сказано, что необходимо найти время, когда тело поднялось на половину максимальной высоты, то давайте и найдем эту максимальную высоту.

Для этого запишем уравнения движения и уравнения скорости в проекции на обе оси.

\[\left\{ \begin{gathered}
ox:x = {v_0}\cos \alpha \cdot t\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1) \hfill \\
oy:y = {v_0}\sin \alpha \cdot t – \frac{{g{t^2}}}{2}\,\,\,(2) \hfill \\
\end{gathered} \right.\]

\[\left\{ \begin{gathered}
ox:{v_x} = {v_0}\cos \alpha \,\,\,\,\,\,\,\,\,\,\,\,(3) \hfill \\
oy:{v_y} = {v_0}\sin \alpha – gt\,\,(4) \hfill \\
\end{gathered} \right.\]

В наивысшей точке подъема вертикальная составляющая скорости равна нулю, поэтому из уравнения (4) найдем время подъема и, подставив его в уравнение (2), получим стандартную формулу для определения максимальной высоты подъема.

\[{v_y} = 0 \Rightarrow {v_0}\sin \alpha  – gt = 0\]

\[t = \frac{{{v_0}\sin \alpha }}{g}\]

\[H = {v_0}\sin \alpha  \cdot t – \frac{{g{t^2}}}{2}\]

\[H = {v_0}\sin \alpha  \cdot \frac{{{v_0}\sin \alpha }}{g} – \frac{g}{2} \cdot \frac{{v_0^2{{\sin }^2}\alpha }}{{{g^2}}}\]

\[H = \frac{{v_0^2{{\sin }^2}\alpha }}{{2g}}\]

А теперь, чтобы найти ответ на поставленный вопрос, воспользуемся второй раз уравнением (2), приняв \(y = \frac{H}{2}\).

\[\frac{H}{2} = {v_0}\sin \alpha  \cdot t_1 – \frac{{g{t_1^2}}}{2}\]

Заменим \(H\) полученной ранее формулой.

\[\frac{{v_0^2{{\sin }^2}\alpha }}{{4g}} = {v_0}\sin \alpha  \cdot {t_1} – \frac{{gt_1^2}}{2}\]

Теперь осталось решить это квадратное уравнение относительно искомого \(t_1\).

\[2{g^2}t_1^2 – 4g{v_0}\sin \alpha  \cdot {t_1} + v_0^2{\sin ^2}\alpha  = 0\]

\[D = 16{g^2}v_0^2{\sin ^2}\alpha  – 4 \cdot 2{g^2} \cdot v_0^2{\sin ^2}\alpha  = 8{g^2}v_0^2{\sin ^2}\alpha \]

\[{t_1} = \frac{{4g{v_0}\sin \alpha  \pm 2\sqrt 2 g{v_0}\sin \alpha }}{{4{g^2}}}\]

Поскольку необходимо найти минимальное время, то нас интересует корень со знаком “минус”.

\[{t_1} = \left( {\frac{{2 – \sqrt 2 }}{2}} \right)\frac{{{v_0}\sin \alpha }}{g}\]

Подставим исходные данные, удостоверившись, что они приведены в системе СИ, и получим численный ответ.

\[{t_1} = \left( {\frac{{2 – \sqrt 2 }}{2}} \right)\frac{{40 \cdot \sin 30^\circ }}{{10}} = 0,59\; с.\]

Ответ: 0,59 с.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Если Вам понравилась задача и ее решение, то Вы можете поделитесь ею с друзьями с помощью этих кнопок.

Смотрите также задачи:

1.6.11 Тело бросили под углом 60 градусов к горизонту со скоростью 10 м/с
1.6.13 Бомбардировщик пикирует на цель под углом 60 градусов к горизонту
1.6.14 Игрок посылает мяч с высоты 1,2 м над землей так, что угол