icodepro.ruУсловие задачи:
Тело, имея некоторую начальную скорость, движется равноускоренно. За время \(t\) тело прошло путь \(S\), причем его скорость увеличилась в \(n\) раз. Найти ускорение тела.
Задача №1.3.39 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(t\), \(S\), \(\frac{\upsilon}{\upsilon_0}=n\), \(a-?\)
Решение задачи:
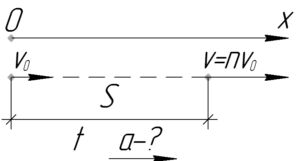Для того чтобы решить задачу, воспользуемся уравнением движения тела и формулой скорости для равноускоренного движения:
\[\left\{ \begin{gathered}
S = {\upsilon _0}t + \frac{{a{t^2}}}{2}\;\;\;\;(1) \hfill \\
\upsilon = {\upsilon _0} + at\;\;\;\;(2) \hfill \\
\end{gathered} \right.\]
Этих двух формул должно быть достаточно. Сначала займемся формулой (2), домножим обе её части на время \(t\).
\[\upsilon t = {\upsilon _0}t + a{t^2}\]
Член \({\upsilon _0}t\) запишем как \(2{\upsilon _0}t – {\upsilon _0}t\), что эквивалентно.
\[\upsilon t = \left( {2{\upsilon _0}t + a{t^2}} \right) – {\upsilon _0}t\]
Теперь, если взглянуть на выражение в скобках и на формулу (1), то видно, что:
\[\upsilon t = 2S – {\upsilon _0}t\]
Все члены с \(t\) переносим в левую часть, выносим за скобки \({\upsilon _0}t\):
\[\upsilon t + {\upsilon _0}t = 2S\]
\[{\upsilon _0}t\left( {\frac{\upsilon }{{{\upsilon _0}}} + 1} \right) = 2S\]
В условии сказано, что скорость тела увеличилась в \(n\) раз, поэтому \(\frac{\upsilon}{\upsilon_0}=n\), а значит:
\[{\upsilon _0}t\left( {n + 1} \right) = 2S\]
Выразим начальную скорость \(\upsilon_0\):
\[{\upsilon _0} = \frac{{2S}}{{t\left( {n + 1} \right)}}\]
Отлично, мы выразили начальную скорость через известные данные задачи. Подставим это выражение в формулу (1).
\[S = \frac{{2S}}{{n + 1}} + \frac{{a{t^2}}}{2}\]
В этом уравнение только одно неизвестное – искомое нами ускорение \(a\), а значит, что после всех преобразований мы сможем его найти.
\[\frac{{nS + S}}{{n + 1}} = \frac{{2S}}{{n + 1}} + \frac{{a{t^2}}}{2}\]
\[\frac{{nS + S}}{{n + 1}} – \frac{{2S}}{{n + 1}} = \frac{{a{t^2}}}{2}\]
\[\frac{{nS + S – 2S}}{{n + 1}} = \frac{{a{t^2}}}{2}\]
\[\frac{{nS – S}}{{n + 1}} = \frac{{a{t^2}}}{2}\]
\[\frac{{S\left( {n – 1} \right)}}{{n + 1}} = \frac{{a{t^2}}}{2}\]
\[a = \frac{{2S\left( {n – 1} \right)}}{{{t^2}\left( {n + 1} \right)}}\]
Ответ: \(\frac{{2S\left( {n – 1} \right)}}{{{t^2}\left( {n + 1} \right)}}\).
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.3.38 Тело, двигаясь с места равноускоренно, проходит за четвертую секунду
1.3.40 Точка движется равноускоренно. За 4 с она проходит путь 24 м. За следующие
1.3.41 Частица, начав двигаться из состояния покоя и пройдя некоторый путь
Все гораздо проще!…
из (1) следует
S/t – at/2 = V0
из (2) следует
at/(n-1) = V0
и после элементарных преобразований следует
a = 2 S (n-1)/( t^2 (n+1))
нельзя ли просто решить с первой формулы? а=(2S-Vot)/(t*t)? Или у нас Vo неизвестен?
Да, начальная скорость нам не дана
аа хорошо, просто я думал что если написан символ V0, значит начальная скорость дана
В самом условии дано лишь во сколько раз конечная скорость больше начальной, начальная скорость не дана
как определить где дано, где не дано?
Из условия задачи
Формула 1 неверна в случае остановки тела и движения в разных направлениях, это формула для разницы координат.
В решении не утверждается обратного, а в условии вообще написано, что тело движется равноускоренно, а это означает, что вектора скорости и ускорения сонаправлены.
Откуда появился nS+S/n+1 вместо S
\[\frac{nS+S}{n+1} = \frac{S\left(n+1\right)}{n+1} = S\]
Это одно и то же, хочу сказать
Почему здесь появилась 2. vt=2S—v0*t??? И куда в последних преобразованиях (во первом действии ) делась S?
Мы имеем:
vt=(2v0*t+at^2)—v0*t
Если посмотреть на выражение в скобках, то видно, что оно равно удвоенному S, ведь S=v0*t+at^2/2 (смотри формулу 1).
Никуда это S дальше не девается, оно же даже присутствует в ответе. Или что Вы имеете ввиду под первым действием?