Решение: Точки окружности вращающегося диска имеют линейную скорость по модулю

Условие задачи:

Точки окружности вращающегося диска имеют линейную скорость по модулю 3 м/с, а точки, находящиеся ближе к оси вращения на 0,1 м, имеют линейную скорость по модулю 2 м/с. Найти угловую скорость вращения диска.

Задача №1.8.22 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\upsilon_1=3\) м/с, \(\Delta R=0,1\) м, \(\upsilon_2=2\) м/с, \(\omega-?\)

Решение задачи:

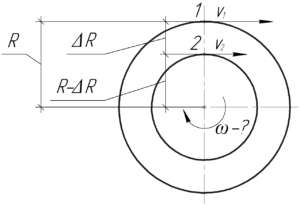Отметим, что все точки диска вращаются с одинаковой угловой скоростью \(\omega\).

Линейная скорость \(\upsilon\) любой точки диска, находящейся на расстоянии \(R\) от оси вращения, в общем случае определяется по формуле:

\[\upsilon = \omega \cdot R\]

Взглянув на рисунок справа, чтобы определить расстояния от оси до соответствующих точек, запишем такую систему.

\[\left\{ \begin{gathered}
{\upsilon _1} = \omega \cdot R \hfill \\
{\upsilon _2} = \omega \cdot \left( {R – \Delta R} \right) \hfill \\
\end{gathered} \right.\]

Вычтем из первой формулы системы вторую.

\[{\upsilon _1} – {\upsilon _2} = \omega \cdot \Delta R\]

\[\omega = \frac{{{\upsilon _1} – {\upsilon _2}}}{{\Delta R}}\]

Численно искомая угловая скорость равна:

\[\omega = \frac{{3 – 2}}{{0,1}} = 10\; рад/с\]