Условие задачи:
Колесо велосипеда делает 100 об/мин. Каков радиус колеса, если скорость велосипедиста равна 4 м/с?
Задача №1.8.9 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\nu=100\) об/мин, \(\upsilon=4\) м/с, \(R-?\)
Решение задачи:
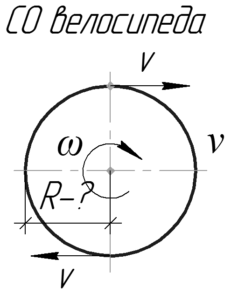 В системе отсчета, связанной с велосипедистом, колесо совершает вращательное движение, при этом скорость крайних точек колеса равна скорости велосипедиста. Это важный факт, так как в системе отсчета Земли оно совершает сложное плоскопараллельное движение.
В системе отсчета, связанной с велосипедистом, колесо совершает вращательное движение, при этом скорость крайних точек колеса равна скорости велосипедиста. Это важный факт, так как в системе отсчета Земли оно совершает сложное плоскопараллельное движение.
Линейная скорость \(\upsilon\) крайних точек колеса связана с угловой скоростью \(\omega\) по формуле:
\[\upsilon = \omega R\;\;\;\;(1)\]
Угловую скорость (её также называют циклической частотой вращения) найдем из частоты вращения согласно выражению:
\[\omega = 2\pi \nu \;\;\;\;(2)\]
Подставим (2) в (1).
\[\upsilon = 2\pi \nu R\]
Выразим необходимый к нахождению радиус \(R\).
\[R = \frac{\upsilon }{{2\pi \nu }}\]
Перед подстановкой данных для расчета в формулу переведем частоту вращения в систему СИ.
\[100\; [1/мин] = \frac{{100}}{{60}}\; [1/с] = \frac{5}{3}\; [1/с]\]
\[R = \frac{4}{{2 \cdot 3,14 \cdot \frac{5}{3}}} = 0,382\; м\]
Ответ: 0,382 м.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.8.8 Во сколько раз изменится центростремительное ускорение тела, если оно будет двигаться
1.8.10 Минутная стрелка часов в 3 раза длиннее секундной. Во сколько раз линейная скорость
1.8.11 Тело движется по окружности с постоянной по модулю скоростью. Во сколько раз

 icodepro.ru
icodepro.ru
Точка соприкосновения колеса и земли является МЦС — мгновенный центр скоростей…
Отсюда и плясать надо…