Условие задачи:
Маленький металлический шарик массой 1 г и зарядом 100 нКл брошен издалека со скоростью 1 м/с в металлическую сферу с зарядом 300 нКл. При каком минимальном значении радиуса сферы шарик достигнет её поверхности?
Задача №6.3.52 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(m=1\) г, \(q=100\) нКл, \(\upsilon=1\) м/с, \(Q=300\) нКл, \(R-?\)
Решение задачи:
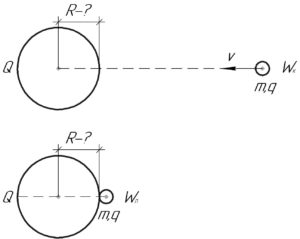 Сделаем важное замечание: при решении задачи мы будем считать, что сфера закреплена (то есть неподвижна)!
Сделаем важное замечание: при решении задачи мы будем считать, что сфера закреплена (то есть неподвижна)!
В момент бросания шарик находит далеко от сферы, поэтому вся энергия системы «шарик-сфера» состоит из кинетической энергии шарика \(W_к\), равной:
\[{W_к} = \frac{{m{\upsilon ^2}}}{2}\]
Когда шарик достигнет сферы, то энергия системы будет складываться из потенциальной энергии взаимодействия зарядов шарика и сферы \(W_п\) и некоторой кинетической энергии шарика. Но если нам нужно найти минимальное значение радиуса сферы, то эта кинетическая энергия будет равна нулю. Потенциальную энергию \(W_п\) найдём по формуле:
\[{W_п} = \frac{{kQq}}{R}\]
Коэффициент пропорциональности \(k\) равен 9·109 Н·м2/Кл2. Согласно закону сохранения энергии \({W_к} = {W_п}\), поэтому:
\[\frac{{m{\upsilon ^2}}}{2} = \frac{{kQq}}{R}\]
Откуда искомый минимальный радиус сферы \(R\) равен:
\[R = \frac{{2kQq}}{{m{\upsilon ^2}}}\]
Произведём расчёты:
\[R = \frac{{2 \cdot 9 \cdot {{10}^9} \cdot 300 \cdot {{10}^{ — 9}} \cdot 100 \cdot {{10}^{ — 9}}}}{{0,001 \cdot {1^2}}} = 0,54\;м\]
Ответ: 0,54 м.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
6.3.51 Электрон, ускоренный разностью потенциалов 5 кВ, влетает в середину зазора между
6.3.53 В электронно-лучевой трубке поток электронов с кинетической энергией 8 кэВ
6.3.54 В закрепленной металлической сфере радиусом 1 см, имеющей заряд -10 нКл

 icodepro.ru
icodepro.ru
А почему при касании сферы шарик обладает именно такой потенциальной энергией(на расстоянии R)? К примеру, какая то часть сферы будет ближе какая то дальше радиуса, и соответственно везде будет оказываться разная потенциальная энергия. Пожалуйста объясните, туплю(
Добрый вечер. Можете уточнить, почему, когда мы бросаем шарик «издалека» он летит по прямой, а не по параболе?
Шарик летел бы по параболе, если на него действовала только сила тяжести. Но есть и сила Кулона. Вообще, траектория не будет ни прямой, ни параболой.