Условие задачи:
Горизонтально расположенный цилиндр разделен скользящей без трения перегородкой на две части. С одной стороны от перегородки находится водород, с другой — гелий. Массы и температуры газов одинаковы. Во сколько раз объем, занимаемый водородом, больше объема, занимаемого гелием?
Задача №4.2.94 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(m_1=m_2=m\), \(T_1=T_2=T\), \(\frac{V_1}{V_2}-?\)
Решение задачи:
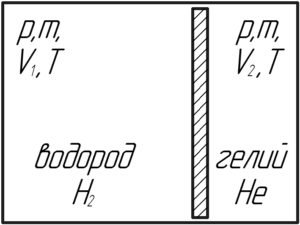 Если внутри цилиндра находится скользящая без трения перегородка, то давления газов по обе стороны от перегородки равны. В противном случае перегородка пришла бы в движение и двигалась бы до тех пор, пока давления газов не стали бы одинаковыми.
Если внутри цилиндра находится скользящая без трения перегородка, то давления газов по обе стороны от перегородки равны. В противном случае перегородка пришла бы в движение и двигалась бы до тех пор, пока давления газов не стали бы одинаковыми.
Запишем уравнение Клапейрона-Менделеева для двух газов:
\[\left\{ \begin{gathered}
p{V_1} = \frac{m}{{{M_1}}}RT \hfill \\
p{V_2} = \frac{m}{{{M_2}}}RT \hfill \\
\end{gathered} \right.\]
Поделим верхнее уравнение на нижнее, чтобы найти искомое отношение объемов \(\frac{V_1}{V_2}\):
\[\frac{{{V_1}}}{{{V_2}}} = \frac{{{M_2}}}{{{M_1}}}\]
Молярная масса водорода \(M_1\) равна 0,002 кг/моль, а гелия \(M_2\) — 0,004 кг/моль.
Посчитаем численное значение искомого отношения:
\[\frac{{{V_1}}}{{{V_2}}} = \frac{{0,004}}{{0,002}} = 2\]
Ответ: 2.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
4.2.93 Два одинаковых сосуда, содержащих газ при 300 К, соединили горизонтальной трубкой
4.2.95 Объем пузырька, всплывающего на поверхность со дна озера, увеличился в два раза
4.2.96 Состояние одного киломоля идеального газа менялось по графику 1-2-3. Определить

 icodepro.ru
icodepro.ru