Решение: На горизонтальном столе по прямой движется шарик. Под каким углом к плоскости стола

Условие задачи:

На горизонтальном столе по прямой движется шарик. Под каким углом к плоскости стола следует установить плоское зеркало, чтобы при движении шарика к зеркалу изображение шарика двигалось по вертикали?

Задача №10.1.21 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\alpha=90^\circ\), \(\beta-?\)

Решение задачи:

Итак, для решения задачи, как и всегда в оптике, нужно сделать рисунок.

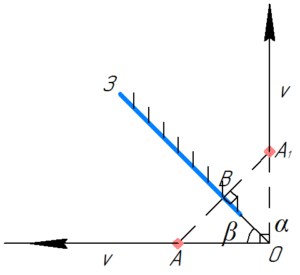
Изобразим шарик A, движущийся по столу, и вектор его скорости \(\upsilon\). Из условия задачи известно, что изображение шарика A₁ в зеркале находится в вертикальной плоскости. Выберем некоторую произвольную точку O в плоскости стола, о назначении которой расскажем чуть позже. Покажем изображение шарика A₁ так, что OA=OA₁, и вектор скорости изображения A₁ направлен вертикально и равен вектору скорости точки.

Точка O – это проекция на плоскость рисунка прямой, образованной при пересечении плоскости зеркала и плоскости стола. Указанное нами условие (OA=OA₁ и равенство векторов точки и её изображения) – это математическое выражение того факта, что зеркало не искажает геометрические размеры.

Далее соединяем точку A с A₁. Так как же изображение предмета в зеркале симметрично самому предмету относительно зеркала, то плоскость зеркала (необязательно само зеркало) проходит через середину отрезка AA₁ (точку B) и точку O.

Треугольники AOB и A₁OB равны друг другу (по двум сторонам и углу между ними), поэтому углы AOB и A₁OB равны друг другу. Значит:

\[\alpha = \beta + \beta \]

\[\alpha = 2\beta \]

\[\beta = \frac{\alpha }{2}\]

Численный ответ равен:

\[\beta = \frac{{90^\circ }}{2} = 45^\circ \]