Условие задачи:
Период дифракционной решетки в два раза больше длины световой волны, нормально падающей на решетку. Определить в градусах угол между максимумами первого порядка.
Задача №10.7.7 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(d=2\lambda\), \(k=1\), \(\gamma-?\)
Решение задачи:
 Запишем формулу дифракционной решетки:
Запишем формулу дифракционной решетки:
\[d\sin \varphi = k\lambda\;\;\;\;(1)\]
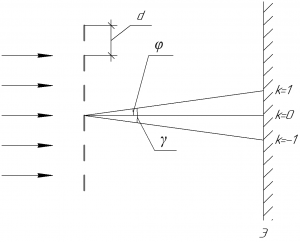
В этой формуле \(d\) — период решетки (также называют постоянной решетки), \(\varphi\) — угол дифракции, \(k\) — порядок максимума (по условию задачи — первые максимумы), \(\lambda\) — длина волны, падающей нормально на решетку.
Из формулы (1) выразим угол дифракции:
\[\sin \varphi = \frac{{k\lambda }}{d}\]
Так как период дифракционной решетки в два раза больше длины световой волны, то есть \(d=2\lambda\), и \(k=1\), то:
\[\sin \varphi = \frac{{1 \cdot \lambda }}{{2\lambda }}\]
\[\sin \varphi = \frac{1}{2}\]
\[\varphi = 30^\circ \]
Искомый угол между первыми максимумами \(\gamma\) можно найти следующим образом (см. рисунок к задаче):
\[\gamma = 2\varphi \]
\[\gamma = 2 \cdot 30^\circ = 60^\circ \]
Ответ: 60°.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
10.7.6 Сколько штрихов на 1 мм должна иметь дифракционная решетка для того, чтобы второй
10.7.8 На дифракционную решетку нормально падает монохроматический свет с длиной волны
10.7.9 На дифракционную решетку с периодом 6 мкм падает монохроматическая волна

 icodepro.ru
icodepro.ru