icodepro.ruУсловие задачи:
По наклонной доске пустили снизу вверх шарик. На расстоянии 30 см от начала пути шарик побывал дважды: через 1 с и через 2 с после начала движения. Определить начальную скорость шарика.
Задача №1.3.45 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(S=30\) см, \(t_1=1\) с, \(t_2=2\) с, \(\upsilon_0-?\)
Решение задачи:
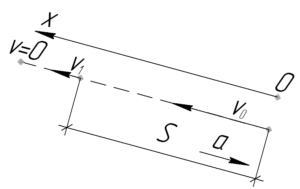Во-первых, если шарик пускали по наклонной доске вверх, то у него определенно была начальная скорость. Во-вторых, в таком случае шарик будет двигаться равнозамедленно. Учитывая все сказанное, запишем уравнение движения шарика.
\[S\left( t \right) = {\upsilon _0}t — \frac{{a{t^2}}}{2}\]
Если шарик побывал на расстоянии \(S\) два раза в момент времени \(t_1\) и \(t_2\), то справедливо записать следующую систему.
\[\left\{ \begin{gathered}
S = {\upsilon _0}{t_1} — \frac{{at_1^2}}{2} \hfill \\
S = {\upsilon _0}{t_2} — \frac{{at_2^2}}{2} \hfill \\
\end{gathered} \right.\]
Подставим числа в систему и найдем начальную скорость. Если решать задачу так, то есть не в общем виде, то нужно следить за тем, чтобы численные значения величин были представлены в системе СИ. Переведем расстояние \(S\) из см в м.
\[30\; см = \frac{{30}}{{100}}\; м = 0,3\; м\]
\[\left\{ \begin{gathered}
0,3 = {\upsilon _0} — 0,5a \hfill \\
0,3 = 2{\upsilon _0} — 2a \hfill \\
\end{gathered} \right.\]
Домножим левую и правую часть верхнего уравнения на 4, затем отнимем из первого уравнения второе и получим ответ к задаче.
\[\left\{ \begin{gathered}
1,2 = 4{\upsilon _0} — 2a \hfill \\
0,3 = 2{\upsilon _0} — 2a \hfill \\
\end{gathered} \right.\]
\[0,9 = 2{\upsilon _0}\]
\[{\upsilon _0} = 0,45\; м/с = 1,62\; км/ч\]
Ответ: 1,62 км/ч.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.3.44 За первую секунду равноускоренного движения тело проходит путь равный 1 м
1.3.46 Тело, двигаясь с начальной скоростью 10 м/с и постоянным ускорением 10 м/с2
1.3.47 Тело, имея начальную скорость 1 м/с, двигаясь равноускоренно, приобрело
А какой путь пройдёт шарик за 2 секунды?
Решение неверное. Как может шарик с одной и той же начальной скоростью и постоянным ускорением дважды пройдя одно и тоже расстояние побывать в точке через разное время? Это возможно когда через 1 с он прошел точку х=30 см при подъеме, а еще через 1с при спуске.
Вы сначала удивленно спрашиваете, как такое вообще возможно, а потом уже сами отвечаете на свой вопрос
Физически же задача очень простая: шарик пускают внизу вверх по наклонной плоскости, в некоторой точке шарик в процессе своего движения побывает дважды (он в принципе в любой точке своей траектории, кроме самой верхней, побывает два раза), нужно найти начальную скорость. Очевидно же, что первый раз он в этой точке будет, когда он движется наверх, а второй раз — когда движется вниз.
А я думаю надо второе уравнение надо записать для ускоренного движения. Тогда появится плюс перед ускорением и уравнения нужно сложить.
В ответе получается 0.25 м/с.
Неееет, так точно неверно
Как будет решатся задача если вместо t2=3 сек?
При подстановке Вы получите уже такую систему:\[\left\{ \begin{gathered}
0,3 = {\upsilon _0} — 0,5a \hfill \\
0,3 = 3{\upsilon _0} — 4,5a \hfill \\
\end{gathered} \right.\]Домножим левую и правую часть верхнего (первого) уравнения на 9, затем отнимем из первого уравнения второе и получим ответ к задаче.\[\left\{ \begin{gathered}
2,7 = 9{\upsilon _0} — 4,5a \hfill \\
0,3 = 3{\upsilon _0} — 4,5a \hfill \\
\end{gathered} \right.\]\[2,4 = 6{\upsilon _0}\]\[{\upsilon _0} = 0,4\;м/с\]
Почему у нас в системе 2 минуса, если сначала шарик катится вверх равнозамедленно, потом вниз равноускорено
Потому что одно уравнение перемещения при равнозамедленном движении описывает движение шарика по наклонной доске, и когда он движется вверх, и когда он движется вниз.
А чему тогда равно ускорение, если начальная скорость 0.45
Полученное значение начальной скорости нужно подставить в любое из двух уравнений системы, тогда найдете ускорение:\[S = {\upsilon _0}{t_1} — \frac{{at_1^2}}{2}\]\[\frac{{at_1^2}}{2} = {\upsilon _0}{t_1} — S\]\[a = \frac{{2\left( {{\upsilon _0}{t_1} — S} \right)}}{{t_1^2}}\]\[a = \frac{{2\left( {0,45 \cdot 1 — 0,3} \right)}}{{{1^2}}} = 0,3\;м/с^2\]
В вашем решении допущена ошибка: 2 уравнение записано неверно, так как путь, пройденный за 2 секунды будет равен S+2*S1, где S — путь, который прошло тело за 1 секунду, а S1 — путь, который прошло тело до полной остановки, правильный ответ V=0,6 м/с
Вы слишком усложняете решение. Одно уравнение описывает движение шарика по наклонной доске: и когда он движется вверх, и когда он движется вниз. Не нужно ничего выдумывать.
А как получилось,что начальную скорость в уравнении умножили на 4?
по-моему мнению нужно было домножить на 4, чтобы ускорения сократились…дальше все делать как как решаются системы
Верно мыслите, я умножал на 4, чтобы далее при вычитании избавиться от ускорения
Почему во втором уравнение есть начальная скорость? Ведь когда он доехал до точки остановки, скорость набиралась только за счет ускорения. Получается его снова толкнули?!
Потому что движение шарика вверх и вниз можно описать одним уравнением.
Вы решали задачи на движение тела, брошенного под углом к горизонту? В таких задачах Вы же не записываете два уравнения для движения тела вверх и вниз, верно?
Где именно был шарик на второй секунде пути ? Он скатился обратно, и пересек точку с которой его запускали пройдя путь S ? Тогда в втором уравнении ускорение положительное, а начальной скорости нет.
И если первое уравнение описывает движение тела не только в верх, но и вниз то что тогда описывает второе уравнение ?
«Так как в одной точке шарик побывал 2 раза»-.как это может быть ?
Ну шарик же пустили снизу вверх, он сначала будет двигаться вверх, потом остановится и начнет движение вниз. Он в принципе в любой точке своего движения вверх побывает два раза — когда катится вверх и когда катится вниз.
Уравнение S(t)=v0*t—a*t^2/2 описывает движение и вверх, и вниз. То, что написано в системе — это вот это же уравнение, просто записанное для двух моментов времени.
Почему два уравнения имеют одинаковые знаки?!! Вверх — РАВНОЗАМЕДЛЕННО, Вниз — РАВНОУСКОРЕННО
У меня одно уравнение, записанное для двух моментов времени
И второй момент прошу пояснить:
Второе равенство для 2 секунд расстояние S разве 30 см будет? Это же пройденный путь за 2 секунды, то есть с начала подъёма до остановки в верхней точке и спуска вниз до точки 30 см от начала подъёма.
Повторяя комментарий ниже: cамое первое уравнение движения (которое S(t)) описывает и движение вверх, и движение вниз, не нужно рассматривать их отдельно.
Почему это так?
Дело в том, что член (v_0*t) — это модуль вектора перемещения вдоль оси x, которое прошёл бы шарик, если бы не было ускорения.
С другой стороны, член (a*t^2/2) — это модуль вектор перемещения шарика против оси x, которое прошёл бы шарик, если двигался равноускоренно, если бы не было начальной скорости.
А итоговое перемещение S — это сумма этих движений (так называемая суперпозиция), т.е. сумма проекций этих векторов.
Так как в одной точке шарик побывал 2 раза, значит перемещение шарика через 1 и 2 секунды было одинаковым.
Дальше, надеюсь, понятно.
Через 2 секунды шарик будет двигаться вниз, то есть равноускоренно. Почему уравнение 2 записано для равно замедленного случая?
Почему оно равнозамедленное? В задаче я говорю, что движение вверх равнозамедленное, о движении вниз — ни слова.
Знак «минус» показывает проекцию ускорения на ось x, но никак не характер ускоренного движения.
Самое первое уравнение движения, написанное в решении, описывает и движение вверх, и движение вниз, не нужно рассматривать их отдельно.
А почему мы из верхнего уравнения вычитаем нижнее?
Можете вычитать наоборот — смысла не меняет, главное избавиться от неизвестного члена 2a.