Условие задачи:
Поезд движется на подъеме со скоростью 10 м/с, а на спуске со скоростью 25 м/с. Определить среднюю скорость поезда на всем пути, если длина спуска в два раза больше длины подъема.
Задача №1.2.4 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\upsilon_1=10\) м/с, \(\upsilon_2=25\) м/с, \(S_2=2S_1\), \(\upsilon_{ср}-?\)
Решение задачи:
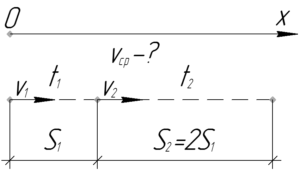 Формула средней скорости применительно к этой задаче будет выглядеть так:
Формула средней скорости применительно к этой задаче будет выглядеть так:
\[{\upsilon _{ср}} = \frac{{{S_1} + {S_2}}}{{{t_1} + {t_2}}}\]
Поезд и на спуске, и на подъеме движется равномерно, но с разной скоростью, поэтому не составит труда найти время подъема \(t_1\) и спуска \(t_2\).
\[{t_1} = \frac{{{S_1}}}{{{\upsilon _1}}}\]
\[{t_2} = \frac{{{S_2}}}{{{\upsilon _2}}}\]
Подставим эти выражения в формулу средней скорости.
\[{\upsilon _{ср}} = \frac{{{S_1} + {S_2}}}{{\frac{{{S_1}}}{{{\upsilon _1}}} + \frac{{{S_2}}}{{{\upsilon _2}}}}}\]
Так как по условию \(S_2=2S_1\), то:
\[{\upsilon _{ср}} = \frac{{{S_1} + 2{S_1}}}{{\frac{{{S_1}}}{{{\upsilon _1}}} + \frac{{2{S_1}}}{{{\upsilon _2}}}}} = \frac{{3{S_1}}}{{\frac{{{S_1}{\upsilon _2} + 2{S_1}{\upsilon _1}}}{{{\upsilon _1}{\upsilon _2}}}}} = \frac{{3{S_1} \cdot {\upsilon _1}{\upsilon _2}}}{{{S_1}\left( {{\upsilon _2} + 2{\upsilon _1}} \right)}} = \frac{{3{\upsilon _1}{\upsilon _2}}}{{2{\upsilon _1} + {\upsilon _2}}}\]
Численный ответ равен:
\[{\upsilon _{ср}} = \frac{{3 \cdot 10 \cdot 25}}{{2 \cdot 10 + 25}} = 16,67\; м/с = 60\; км/ч\]
Ответ: 60 км/ч.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.2.3 За минуту человек делает сто шагов. Определить скорость движения человека, если
1.2.5 Автобус третью часть пути шел со скоростью 20 км/ч, половину оставшегося пути
1.2.6 Движение грузового автомобиля описывается уравнением x=-270+12t (м). Когда

 icodepro.ru
icodepro.ru
Ты красавчик
По условию задачи, S1=1, а в конце вы в знаменателе умножает на 2, и если так, то и скобки раскрыли неправильно
Я все перепроверил, ошибок здесь нет.
Что такое S1=1?
Там ответ 17 метров в секунду
60 км/ч — это и есть примерно 17 м/с