Условие задачи:
Протон влетает в однородное магнитное поле перпендикулярно линиям магнитной индукции и начинает двигаться по окружности. Как изменится частота вращения протона, если величину индукции магнитного поля уменьшить в два раза?
Задача №8.2.28 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\alpha=90^\circ\), \(B_2=\frac{1}{2}B_1\), \(\frac{\nu_2}{\nu_1}-?\)
Решение задачи:
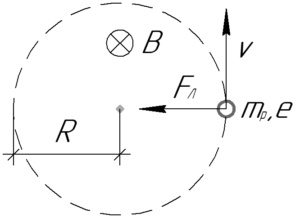 Под действием силы Лоренца протон в магнитном поле будет совершать равномерное движение по окружности. Очевидно, что если протон движется по окружности радиуса \(R\) со скоростью \(\upsilon\), то период обращения \(T\), то есть время, за которое протон сделает один оборот (или пройдет одну длину окружности, равную \(2\pi R\)), можно найти так:
Под действием силы Лоренца протон в магнитном поле будет совершать равномерное движение по окружности. Очевидно, что если протон движется по окружности радиуса \(R\) со скоростью \(\upsilon\), то период обращения \(T\), то есть время, за которое протон сделает один оборот (или пройдет одну длину окружности, равную \(2\pi R\)), можно найти так:
\[T = \frac{{2\pi R}}{\upsilon }\]
Частоту вращения протона \(\nu\) можно найти как величину, обратную периоду обращения \(T\):
\[\nu = \frac{1}{T}\]
\[\nu = \frac{\upsilon }{{2\pi R}}\;\;\;\;(1)\]
Силу Лоренца \(F_Л\) определяют по следующей формуле:
\[{F_Л} = B\upsilon e\sin \alpha \;\;\;\;(2)\]
Здесь \(B\) — индукция магнитного поля, \(\upsilon\) — скорость протона, \(e\) — модуль заряда протона, \(\alpha\) — угол между вектором скорости и вектором магнитной индукции.
Направление действия силы Лоренца определяется правилом левой руки: если ладонь левой руки расположить так, чтобы линии магнитной индукции входили в нее, а четыре вытянутых пальца направить по направлению движения положительного заряда (или против направления отрицательного заряда), то большой палец, оставленный на 90°, покажет направление силы Лоренца. В нашем случае (при таком направлении вектора магнитной индукции) сила Лоренца направлена влево.
Сила Лоренца \(F_Л\) сообщает протону центростремительное ускорение \(a_ц\), поэтому из второго закона Ньютона следует, что:
\[{F_Л} = {m_p}{a_ц}\;\;\;\;(3)\]
Центростремительное ускорение \(a_ц\) можно определить через скорость \(\upsilon\) и радиус кривизны траектории \(R\) по формуле:
\[{a_ц} = \frac{{{\upsilon ^2}}}{R}\;\;\;\;(4)\]
Подставим (4) в (3), тогда:
\[{F_Л} = \frac{{{m_p}{\upsilon ^2}}}{R}\;\;\;\;(5)\]
Приравняем правые части (2) и (5):
\[B\upsilon e\sin \alpha = \frac{{{m_p}{\upsilon ^2}}}{R}\]
Имеем:
\[Be\sin \alpha = \frac{{{m_p}\upsilon }}{R}\]
Откуда отношение \(\frac{\upsilon}{R}\), которое нам будет нужно в ходе дальнейшего решения, равно:
\[\frac{\upsilon }{R} = \frac{{Be\sin \alpha }}{{m_p}}\]
Полученное выражение подставим в (1):
\[\nu = \frac{{Be\sin \alpha }}{{2\pi {m_p}}}\]
Запишем полученную формулу дважды для двух случаев, описанных в условии задачи:
\[\left\{ \begin{gathered}
{\nu _1} = \frac{{{B_1}e\sin \alpha }}{{2\pi {m_p}}} \hfill \\
{\nu _2} = \frac{{{B_2}e\sin \alpha }}{{2\pi {m_p}}} \hfill \\
\end{gathered} \right.\]
Поделим нижнее равенство на верхнее, тогда искомое отношение \(\frac{\nu_2}{\nu_1}\) равно:
\[\frac{{{\nu _2}}}{{{\nu _1}}} = \frac{{{B_2}}}{{{B_1}}}\]
По условию величину индукции магнитного поля уменьшают в два раза, то есть \(B_2=\frac{1}{2}B_1\), поэтому:
\[\frac{{{\nu _2}}}{{{\nu _1}}} = \frac{B_1}{2B_1} = \frac{1}{2}\]
Ответ: \(\frac{{{\nu _2}}}{{{\nu _1}}} = \frac{1}{2}\).
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
8.2.27 Протон и дейтрон (ядро изотопа водорода 2H1) влетают в однородное магнитное поле
8.3.1 Сила тока в плоском контуре возрастает в 2 раза. Во сколько раз увеличивается
8.3.2 Поток магнитной индукции, пронизывающий плоскость квадрата, равен 0,2 Вб. Каким

 icodepro.ru
icodepro.ru