Условие задачи:
Середина стержня, имеющего длину 10 мм, находится на расстоянии 18 см от собирающей линзы на её главной оптической оси. Фокусное расстояние линзы 12 см. Определите длину изображения стержня, если он расположен вдоль главной оптической оси линзы.
Задача №10.5.62 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(l=10\) мм, \(d=18\) см, \(F=12\) см, \(L-?\)
Решение задачи:
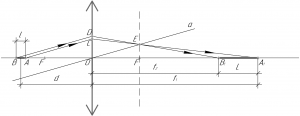 Чтобы решить задачу, нужно построить изображение обоих концов стержня, тогда длину изображения стержня можно определить по формуле (это прекрасно видно из рисунка):
Чтобы решить задачу, нужно построить изображение обоих концов стержня, тогда длину изображения стержня можно определить по формуле (это прекрасно видно из рисунка):
\[L = {f_1} — {f_2}\;\;\;\;(1)\]
Покажем общий принцип построения изображения точки в собирающей линзе. Чтобы построить изображение точки A в собирающей линзе, нужно провести через точку A некоторый луч, этот луч пересечет линзу в точке C. Далее через главный оптический центр O проведем прямую a параллельную лучу AC, которая пересечет заднюю фокальную плоскость в точке E. Далее необходимо провести через точки C и E прямую, которая пересечет главную оптическую ось в точке A1. Точка A1 и есть изображение точки A в собирающей линзе. Изображение точки B строится аналогичным образом.
Запишем формулу тонкой линзы в общем случае:
\[\frac{1}{F} = \frac{1}{d} + \frac{1}{f}\]
В этой формуле \(F\) — фокусное расстояние линзы, знак перед ним «+», поскольку линза — собирающая, \(d\) — расстояние от линзы до предмета, знак перед ним «+», поскольку предмет — действительный (в случае одиночной линзы предмет всегда действительный, оно бывает мнимым в случае системы линз), \(f\) — расстояние от линзы до изображения, знак перед ним «+», поскольку изображение — действительное (то есть образуется на сходящемся пучке лучей — смотрите рисунок).
Применительно к точкам A и B формула примет следующий вид:
\[\left\{ \begin{gathered}
\frac{1}{F} = \frac{1}{{d — 0,5l}} + \frac{1}{{{f_1}}} \hfill \\
\frac{1}{F} = \frac{1}{{d + 0,5l}} + \frac{1}{{{f_2}}} \hfill \\
\end{gathered} \right.\]
Тогда:
\[\left\{ \begin{gathered}
\frac{1}{{{f_1}}} = \frac{1}{F} — \frac{1}{{d — 0,5l}} \hfill \\
\frac{1}{{{f_2}}} = \frac{1}{F} — \frac{1}{{d + 0,5l}} \hfill \\
\end{gathered} \right.\]
\[\left\{ \begin{gathered}
\frac{1}{{{f_1}}} = \frac{{d — 0,5l — F}}{{F\left( {d — 0,5l} \right)}} \hfill \\
\frac{1}{{{f_2}}} = \frac{{d + 0,5l — F}}{{F\left( {d + 0,5l} \right)}} \hfill \\
\end{gathered} \right.\]
\[\left\{ \begin{gathered}
{f_1} = \frac{{F\left( {d — 0,5l} \right)}}{{\left( {d — F} \right) — 0,5l}} \hfill \\
{f_2} = \frac{{F\left( {d + 0,5l} \right)}}{{\left( {d — F} \right) + 0,5l}} \hfill \\
\end{gathered} \right.\]
Подставим полученные выражения в формулу (1):
\[L = \frac{{F\left( {d — 0,5l} \right)}}{{\left( {d — F} \right) — 0,5l}} — \frac{{F\left( {d + 0,5l} \right)}}{{\left( {d — F} \right) + 0,5l}}\]
Приведем под общий знаменатель:
\[L = \frac{{F\left( {d — 0,5l} \right)\left( {\left( {d — F} \right) + 0,5l} \right) — F\left( {d + 0,5l} \right)\left( {\left( {d — F} \right) — 0,5l} \right)}}{{\left( {\left( {d — F} \right) — 0,5l} \right)\left( {\left( {d — F} \right) + 0,5l} \right)}}\]
\[L = \frac{{F\left( {d — 0,5l} \right)\left( {\left( {d + 0,5l} \right) — F} \right) — F\left( {d + 0,5l} \right)\left( {\left( {d — 0,5l} \right) — F} \right)}}{{\left( {\left( {d — F} \right) — 0,5l} \right)\left( {\left( {d — F} \right) + 0,5l} \right)}}\]
В числителе раскроем скобки, в знаменателе видим разность квадратов:
\[L = \frac{{F\left( {d — 0,5l} \right)\left( {d + 0,5l} \right) — {F^2}\left( {d — 0,5l} \right) — F\left( {d + 0,5l} \right)\left( {d — 0,5l} \right) + {F^2}\left( {d + 0,5l} \right)}}{{{{\left( {d — F} \right)}^2} — 0,25{l^2}}}\]
Окончательно получим такое решение задачи в общем виде:
\[L = \frac{{{F^2}l}}{{{{\left( {d — F} \right)}^2} — 0,25{l^2}}}\]
Посчитаем численный ответ:
\[L = \frac{{{{0,12}^2} \cdot 0,01}}{{{{\left( {0,18 — 0,12} \right)}^2} — 0,25 \cdot {{0,01}^2}}} = 0,04\;м = 4\;см\]
Ответ: 4 см.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
10.5.61 Светящаяся точка находится в фокусе рассеивающей линзы. На каком расстоянии от линзы
10.5.63 Точечный источник света находится на расстоянии 40 см от собирающей линзы с фокусным
10.5.64 На расстоянии 60 см от собирающей линзы с фокусным расстоянием 50 см находится

 icodepro.ru
icodepro.ru