icodepro.ruУсловие задачи:
Скорость велосипедиста 36 км/ч, а скорость встречного ветра 4 м/с. Какова скорость ветра в системе отсчета, связанной с велосипедистом?
Задача №1.7.6 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\upsilon_1=36\) км/ч, \(\upsilon_2=4\) м/с, \(\upsilon_{21}-?\)
Решение задачи:
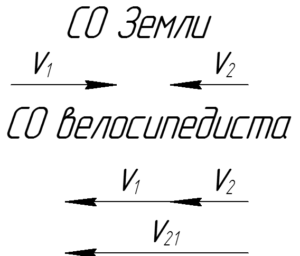Посмотрим на рисунок к решению задачи, приведенный справа. В условии скорость велосипедиста и ветра даны в системе отсчета Земли (СО Земли). Для того, что перейти в систему отсчета велосипедиста, необходимо к вектору скорости ветра \(\overrightarrow {{\upsilon _2}}\) прибавить вектор, равный вектору скорости велосипедиста и направленный противоположно ему, т.е. \(— \overrightarrow {{\upsilon _1}} \). Таким образом мы как бы мысленно останавливаем велосипедиста. В итоге, модуль вектора скорости ветра в СО велосипедиста равен:
\[{\upsilon _{21}} = {\upsilon _1} + {\upsilon _2}\]
Переведем скорость велосипедиста в единицы системы СИ, т.е. из км/ч в м/с.
\[36\; км/ч = \frac{{36 \cdot 1000}}{{1 \cdot 3600}}\; м/с = \frac{{360}}{{36}}\; м/с = 10\; м/с\]
\[{\upsilon _{21}} = 10 + 4 = 14\; м/с = 50,4\; км/ч\]
Ответ: 50,4 км/ч.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.7.5 По оси x движутся две точки: первая по закону x1=10+2t, а вторая — по закону
1.7.7 Танк движется со скоростью 20 км/ч. С какими скоростями относительно дороги
1.7.8 Два поезда идут навстречу друг другу со скоростями 36 и 54 км/ч. Пассажир
Добрый день. Нужно второе мнение при решении такой задачи.
Два велосипедиста проехали дистанцию 3480 км со след результатами: Вел1 = 82 часа, Вел2 = 86 часов. Скорость встречного ветра 3 м\с
Вопрос: какие результаты они покажут, если у первого скорость ветра будет на 10% больше, а у второго на 10% меньше.
Вроде понятно как решать, но смущает линейность.
В моем решении получилось, что при таких изменениях встречного ветра, второй приедет быстрее.
Заранее признателен
Надеюсь понятно, что собственную скорость любого из велосипедистов можно найти по формуле: \[\upsilon = \frac{S}{t} + {\upsilon _в} = \frac{{S + {\upsilon _в}t}}{t}\] Если скорость скорость ветра будет изменяться на \(\alpha \) процентов (выражается в долях, например 10%=0,1, также не забываем знак, то есть если скорость уменьшается, то \(\alpha \) — отрицательное), то время \(\tau\), за которое каждый велосипедист пройдет дистанцию, можно определить по формуле:\[\tau = \frac{S}{{\upsilon — \left( {1 + \alpha } \right){\upsilon _в}}}\]Учитывая ранее полученное, имеем:\[\tau = \frac{S}{{\frac{{S + {\upsilon _в}t}}{t} — \left( {1 + \alpha } \right){\upsilon _в}}}\]Домножим и числитель, и знаменатель на \(t\), тогда:\[\tau = \frac{{St}}{{S + {\upsilon _в}t — \left( {1 + \alpha } \right){\upsilon _в}t}}\]\[\tau = \frac{{St}}{{S — \alpha {\upsilon _в}t}}\]Считаем:\[{\tau _1} = \frac{{3480 \cdot 82}}{{3480 — 0,1 \cdot 10,8 \cdot 82}} = 84,14\;ч\]\[{\tau _2} = \frac{{3480 \cdot 86}}{{3480 + 0,1 \cdot 10,8 \cdot 86}} = 83,76\;ч\]Как-то так
Шикарно.
У меня тоже были такие ответы, но конечно не так красиво полученные.
Но вот в чем вопрос. Данное решение, возможно, не универсально, так как в реальной жизни у велосипедиста есть ограничение по работе, которую он может совершить. Чем больше скорость, тем больше работа (вот наверное где нелинейность) То есть ехать с большой скоростью более утомительно, чем с малой… При этом энергия конечна (устал и не может ехать).. Не пойму как это все увязать.
И вообще, есть ли смысл\возможность решать задачу в таком контексте? Было бы интересно.
Смысл то решать есть, но вот в физике я разбираюсь гораздо лучше, чем в физиологии.
Вот если бы Вам были даны эти зависимости, то Вы бы могли решить задачи. Но в данном случае решаете так, как и делали.
Как мне кажется, физиология в данном случае очень сложна. Простой пример: подтянуться 5 раз гораздо легче, чем поднять штангу 300 кг, хотя работа примерно одинакова (или я ошибаюсь?).
Скорость велосипедиста 36 км/ч — это скорость его с учетом ветра? или скорость в безветренную погоду?
Это собственная скорость велосипедиста или его скорость в безветренную погоду.
Почему в задаче не указано: попутный это или встречный ветер? От этого зависит решение: v21=v1-v2 либо v21=v1+v2.
В условии написано «скорость встречного ветра», читайте внимательно!
А в целом мыслите правильно, от этого действительно зависит решение задачи
не значит ли это что мы должны от скорости велосипедиста отнять скорость ветра он же против ветра едет
Совсем нет. Попробуйте принять скорости велосипедиста и ветра равными. Если действовать, как предлагаете Вы, то относительная скорость будет равна нулю, т.е. велосипедист не должен чувствовать ветра. А теперь вернитесь к жизни. Вы едите на велосипеде со скоростью, например, 10 км/ч, и Вам дует встречный ветер такой же скорости. Думаете, Вы не будете чувствовать ветер?
А вообще, правило перехода из одной системы отсчета в другую я описал в решении.