Условие задачи:
Спортсменка, стоящая на вышке, бросает мяч с горизонтальной скоростью 15 м/с. Бросая мяч, она теряет равновесие и падает с вышки, достигая воды через 1 с. С какой скоростью мяч упадет в воду?
Задача №1.5.10 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\upsilon_0=15\) м/с, \(t=1\) с, \(\upsilon-?\)
Решение задачи:
Очевидно, что и мяч, и спортсменка достигнут поверхности воды за одинаковое время, поскольку оно зависит только от высоты падения, а она одинакова. Неверно думать, что чем больше масса, тем быстрее тело упадет! Это было доказано еще Галилео Галилеем, который бросал шары разной массы с той самой наклоненной Пизанской башни.
Разложим скорость мяча, с которой он упадет в воду, на вертикальную \(\upsilon_y\) и горизонтальную \(\upsilon_x\) составляющие. Тогда саму конечную скорость можно найти из теоремы Пифагора:
\[\upsilon = \sqrt {\upsilon _x^2 + \upsilon _y^2}\,\,\,(1) \]
Запишем уравнения скорости, спроецированные на оси координат:
\[\left\{ \begin{gathered}
ox:{\upsilon _x} = {\upsilon _0}\,\,\,(2) \hfill \\
oy:{\upsilon _y} = gt\,\,\,(3) \hfill \\
\end{gathered} \right.\]
Подставим выражения (2) и (3) в (1), тогда получим формулу для вычисления ответа:
\[\upsilon = \sqrt {\upsilon _0^2 + {g^2}{t^2}} \]
\[\upsilon = \sqrt {{{15}^2} + {{10}^2}{1^2}} = 18,03\; м/с \approx 65\; км/ч \]
Ответ: 65 км/ч.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.5.9 Тело брошено с высоты 2 м горизонтально так, что к поверхности земли
1.5.11 Тело брошено горизонтально с высоты h=20 м. Траектория его движения
1.6.1 Тело брошено со скоростью 10 м/с под углом 30 градусов к горизонту

 icodepro.ru
icodepro.ru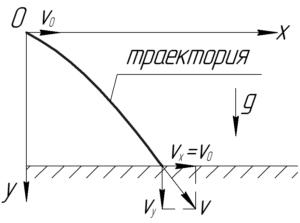
бедная девушка

Простите, не могу понять, почему мяч и спортсменка достигают поверхности воды за одно и тоже время. То, что у мяча есть начальная горизонтальная скорость никак не сказывается на времени?
Горизонтальная скорость не оказывает никакого влияния на движение вдоль вертикальной оси
Спасибо большое