Чашки равноплечих весов находятся в воде плотностью 1 г/см3. Найти массу гирь

Условие задачи:

Чашки равноплечих весов находятся в воде плотностью 1 г/см³. Найти массу гирь, изготовленных из сплава плотностью 7 г/см³, которые уравновесят тело массой 1 кг и объемом 100 см³.

Задача №3.3.39 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\rho_в=1\) г/см³, \(\rho=7\) г/см³, \(M=1\) кг, \(V_1=100\) см³, \(m-?\)

Решение задачи:

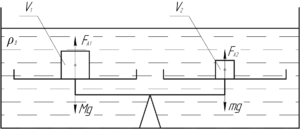Если равноплечие весы будут находиться в равновесии, значит на левую и правую чаши весов действуют одинаковые по величине силы, то есть верно следующее равенство (смотрите схему):

\[Mg – {F_{А1}} = mg – {F_{А2}}\]

Распишем силы Архимеда \(F_{А1}\) и \(F_{А2}\) в левой и правой части равенства по известной формуле:

\[Mg – {\rho _в}g{V_1} = mg – {\rho _в}g{V_2}\]

\[M – {\rho _в}{V_1} = m – {\rho _в}{V_2}\]

Неизвестный объем \(V_2\) можно выразить из массы \(m\) и плотности \(\rho\) по формуле:

\[{V_2} = \frac{m}{\rho }\]

\[M – {\rho _в}{V_1} = m – {\rho _в}\frac{m}{\rho }\]

\[M – {\rho _в}{V_1} = \frac{{m\left( {\rho  – {\rho _в}} \right)}}{\rho }\]

Выразим неизвестную массу гирь \(m\):

\[m = \frac{{\rho \left( {M – {\rho _в}{V_1}} \right)}}{{\rho  – {\rho _в}}}\]

Переведем плотности и объем тела в систему СИ:

\[1\;г/см^3 = 1000\;кг/м^3\]

\[7\;г/см^3 = 7000\;кг/м^3\]

\[100\;см^3 = {10^{ – 4}}\;м^3\]

Посчитаем численный ответ к задаче:

\[m = \frac{{7000 \cdot \left( {1 – 1000 \cdot {{10}^{ – 4}}} \right)}}{{7000 – 1000}} = 1,05\;кг\]

Ответ: 1,05 кг.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

3.3.38 С какой высоты должно падать тело плотностью 400 кг/м3, чтобы оно погрузилось
3.3.40 Человек прыгает в воду со скалы высотой 10 м. На какую глубину он опустится
3.3.41 Шарик подвесили на упругой пружине и опустили в воду. Во сколько раз уменьшилось