Условие задачи:
На рычажных весах уравновешен сосуд с водой. На сколько нужно увеличить массу гирь для восстановления равновесия, если в воду погрузить подвешенный на нитке стальной брусок размером 5 см x 6 см x 8 см так, чтобы он не касался дна?
Задача №3.3.34 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(a=5\) см, \(b=6\) см, \(c=8\) см, \(m-?\)
Решение задачи:
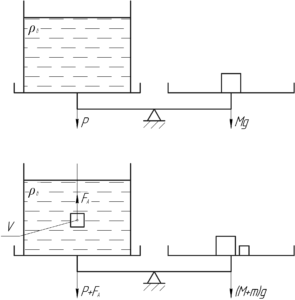 Изначально на левом плече рычажных весов находился сосуд с водой, а на правом – некоторое количество гирь массой \(M\), при этом вес сосуда с водой \(P\) был уравновешен весом гирь \(Mg\), то есть:
Изначально на левом плече рычажных весов находился сосуд с водой, а на правом – некоторое количество гирь массой \(M\), при этом вес сосуда с водой \(P\) был уравновешен весом гирь \(Mg\), то есть:
\[P = Mg\;\;\;\;(1)\]
Далее в сосуд погружают стальной брусок. На него со стороны воды действует сила Архимеда \(F_А\). Но важно то, что и сам брусок действует на воду с такой же по величине силой (но другого направления) согласно третьему закону Ньютона. Поэтому понятно, что на левое плечо уже действует сила \(\left( {P + {F_А}} \right)\), поэтому на правое плечо нужно добавить несколько гирь искомой массы \(m\).
\[P + {F_А} = \left( {M + m} \right)g\;\;\;\;(2)\]
Вычтем из равенства (2) равенство (1):
\[{F_А} = mg\]
Распишем силу Архимеда:
\[{\rho _в}gV = mg\]
\[m={\rho _в}V\]
Объем бруска \(V\) можно найти как произведение длин всех его ребер, поэтому окончательно имеем такую формулу:
\[m = {\rho _в}abc\]
Плотность воды \(\rho_в\) равна 1000 кг/м3. Переведем длины ребер в систему СИ и посчитаем ответ:
\[5\;см = 0,05\;м\]
\[6\;см = 0,06\;м\]
\[8\;см = 0,08\;м\]
\[m = 1000 \cdot 0,05 \cdot 0,06 \cdot 0,08 = 0,24\;кг\]
Ответ: 0,24 кг.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
3.3.33 Деревянный шар лежит на дне сосуда с водой, причем половина его находится в воде
3.3.35 Поверх жидкости плотностью 1000 кг/м3 налита большим слоем жидкость плотностью
3.3.36 Полый железный шар взвешивают в воздухе и керосине. Показания динамометра

 icodepro.ru
icodepro.ru