icodepro.ruУсловие задачи:
Полый цинковый шар, внешний объем которого 200 см3, плавает так, что половина его находится в воде. Определить объем свободного пространства шара.
Задача №3.3.27 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(V=200\) см3, \(V_{п}=0,5V\), \(V_{пол}-?\)
Решение задачи:
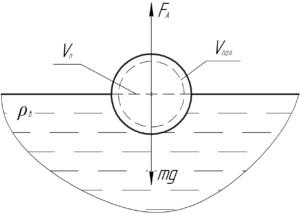Так как шар плавает, то запишем условие плавания тел:
\[{F_А} = mg\;\;\;\;(1)\]
Сила Архимеда определяется по такой формуле:
\[{F_А} = {\rho _в}g{V_п}\]
Так как цинковый шар наполовину погружен в воду (\(V_{п}=0,5V\)), то:
\[{F_А} = 0,5{\rho _в}gV\;\;\;\;(2)\]
Плотность воды \(\rho_в\) равна 1000 кг/м3.
Масса шара равна произведению плотности цинка (\(\rho=7100\) кг/м3) на объем шара без полости, которая, очевидно, равна \(\left( {V – {V_{пол}}} \right)\).
\[m = \rho \left( {V – {V_{пол}}} \right)\;\;\;\;(3)\]
В равенство (1) подставим выражения (2) и (3):
\[0,5{\rho _в}gV = \rho \left( {V – {V_{пол}}} \right)g\]
\[0,5{\rho _в}V = \rho \left( {V – {V_{пол}}} \right)\]
\[V – {V_{пол}} = \frac{{{\rho _в}V}}{{2\rho }}\]
\[{V_{пол}} = V\left( {1 – \frac{{{\rho _в}}}{{2\rho }}} \right)\]
Если не переводить объем шара в систему СИ, то мы получим ответ в см3. Посчитаем объем свободного пространства шара.
\[{V_{пол}} = 200 \cdot \left( {1 – \frac{{1000}}{{2 \cdot 7100}}} \right) = 186\;см^3\]
Ответ: 186 см3.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
3.3.26 Плотность жидкости в 3 раза больше плотности материала тела. Какая часть объема
3.3.28 Стеклянный шарик объемом 0,5 см3 равномерно тонет в воде. Какое количество
3.3.29 Тело массой 2 кг и объемом 1 л находится в озере на глубине 5 м. Какую необходимо
а откуда 7100, я не поняла
В равенство (1) подставим выражения (2) и (3):
Распишите этот пункт кому не жалко, пожалуйста
У тебя есть такое равенство (1):\[{F_А} = mg\]Ты вместо силы Архимеда пишешь \(0,5{\rho _в}gV\), а вместо массы – \(\rho \left( {V – {V_{пол}}} \right)\). Тогда получишь:\[0,5{\rho _в}gV = \rho \left( {V – {V_{пол}}} \right)g\]
Куда пропадает минус при перенесении объема вправо?
\[V – {V_{пол}} = \frac{{{\rho _в}V}}{{2\rho }}\]\[ – {V_{пол}} = \frac{{{\rho _в}V}}{{2\rho }} – V\]\[{V_{пол}} = V – \frac{{{\rho _в}V}}{{2\rho }}\]\[{V_{пол}} = V\left( {1 – \frac{{{\rho _в}}}{{2\rho }}} \right)\]
Спасибо , лучшего объяснения быть не может!!!!!!!!!!!!!
А откуда единица взялась в конце?
Объем V был вынесен как общий множитель за скобки, так в скобках появилась единица
а можно поподробнее объяснит ?)
Из третьей формулы, если считать снизу, следует, что:
\[{V_{пол}} = V – V\frac{{{\rho _в}}}{{2\rho }} = V\left( {1 – \frac{{{\rho _в}}}{{2\rho }}} \right)\]
А откуда появились 2 плотности цинка?
И вообще откуда появилась плотность цинка если мы используем формулу Архимеда?
Вообще мы используем условие плавания тел, об этом говорится в решении. Плотность цинка появляется при нахождении массы полого шара, которая нужна при нахождении силы тяжести mg.
Двойка появилась при математических преобразованиях, читайте решение.
Спасибо за объяснение.
Я не чего не понял
Откуда тут 2 я не поняла
Я 0,5 представляю как дробь 1/2, так и появляется двойка.