Условие задачи:
Шарик от настольного тенниса диаметром 4 см и массой 8 г удерживается под водой на глубине 40 см. Если его отпустить, то он поднимется над поверхностью воды на высоту 1 м. Определить работу шарика против силы сопротивления воды.
Задача №3.3.45 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(d=4\) см, \(m=8\) г, \(h=40\) см, \(H=1\) м, \(A-?\)
Решение задачи:
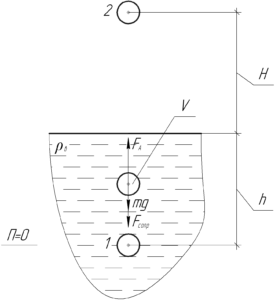 Работа шарика против силы сопротивления воды равна работе этой силы, взятой с противоположным знаком.
Работа шарика против силы сопротивления воды равна работе этой силы, взятой с противоположным знаком.
\[A = — {A_{сопр}}\;\;\;\;(1)\]
Для решения этой задачи следует воспользоваться законом сохранения энергии. Замечу, что на шарик действуют две неконсервативные силы: сила Архимеда \(F_{А}\) и сила сопротивления воды \(F_{сопр}\). Эти силы будут совершать работу. Сумма этих работ равна изменению полной механической энергии, то есть:
\[{A_{Арх}} + {A_{сопр}} = \Delta E\]
\[{A_{сопр}} = \Delta E — {A_{Арх}}\]
Если учесть (1), то получим:
\[A = {A_{Арх}} — \Delta E\;\;\;\;(2)\]
Поскольку в точках 1 и 2 у шарика нет скорости, то изменение полной механической энергии равно изменению потенциальной энергии. Если выбрать уровень отсчета потенциальной энергии в точке 1, то:
\[\Delta E = mg\left( {H + h} \right)\;\;\;\;(3)\]
Если пренебрежем участком выхода шарика из воды, когда сила Архимеда \(F_{А}\) переменна, то работу этой силы можно находить из выражения:
\[{A_{Арх}} = {F_А} \cdot h\]
Распишем силу Архимеда \(F_{А}\) по известной формуле:
\[{A_{Арх}} = {\rho _в}gV \cdot h\]
Поскольку \(r = \frac{d}{2}\), то объем шарика можно находить так:
\[V = \frac{4}{3}\pi {r^3}\]
\[V = \frac{4}{3}\pi {\left( {\frac{d}{2}} \right)^3} = \frac{{\pi {d^3}}}{6}\]
Тогда:
\[{A_{Арх}} = {\rho _в}g\frac{{\pi {d^3}}}{6} \cdot h\;\;\;\;(4)\]
Подставим выражения (3) и (4) в формулу (1). В итоге имеем:
\[A = {\rho _в}g\frac{{\pi {d^3}}}{6} \cdot h — mg\left( {H + h} \right)\]
Произведем вычисления, произведя перед этим перевод некоторых величин в систему СИ:
\[4\;см = 0,04\;м\]
\[8\;г = 0,008\;кг\]
\[40\;см = 0,4\;м\]
\[A = 1000 \cdot 10 \cdot \frac{{3,14 \cdot {{0,04}^3}}}{6} \cdot 0,4 — 0,008 \cdot 10 \cdot \left( {1 + 0,4} \right) = 0,022\;Дж = 22\;мДж\]
Ответ: 22 мДж.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
3.3.44 Цилиндр плавает в вертикальном положении в сосуде с водой. В сосуд подливают более
3.3.46 В воде плавает льдина с площадью поперечного сечения 5 м2 и высотой 0,5 м. Какую
3.3.47 Однородный куб плавает в воде, на 0,75 своего объема погрузившись в воду. Если

 icodepro.ru
icodepro.ru