Условие задачи:
Шарик подвесили на упругой пружине и опустили в воду. Во сколько раз уменьшилось удлинение пружины, если плотность шарика в три раза больше плотности воды?
Задача №3.3.41 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\rho = 3 \rho_в\), \(\frac{x_1}{x_2}-?\)
Решение задачи:
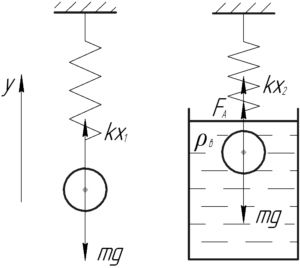 В первом случае на шарик действуют сила тяжести \(mg\) и сила упругости \(kx_1\) (пружина растянута на величину \(x_1\)).
В первом случае на шарик действуют сила тяжести \(mg\) и сила упругости \(kx_1\) (пружина растянута на величину \(x_1\)).
Когда шарик погрузят в воду, то на шарик начнёт действовать ещё и сила Архимеда \(F_А\), поэтому деформация пружины уменьшится до величины \(x_2\). На шарик теперь действуют сила тяжести \(mg\), сила упругости \(kx_2\) и сила Архимеда \(F_А\).
Шарик в обоих случаях находится в равновесии, запишем первый закон Ньютона в проекции на ось \(y\):
\[\left\{ \begin{gathered}
k{x_1} — mg = 0 \hfill \\
k{x_2} + {F_А} — mg = 0 \hfill \\
\end{gathered} \right.\]
Перепишем в более удобный для нас вид, далее Вы увидите, зачем мы это сделали:
\[\left\{ \begin{gathered}
mg = k{x_1} \hfill \\
mg — {F_А} = k{x_2} \hfill \\
\end{gathered} \right.\]
Поделим верхнее равенство на нижнее:
\[\frac{{{x_1}}}{{{x_2}}} = \frac{{mg}}{{mg — {F_А}}}\]
Массу представим как произведение плотности материала шарика \(\rho\) на полный объем \(V\), силу Архимеда \(F_А\) распишем по формуле-определению.
\[\frac{{{x_1}}}{{{x_2}}} = \frac{{\rho Vg}}{{\rho Vg — {\rho _в}gV}}\]
\[\frac{{{x_1}}}{{{x_2}}} = \frac{\rho }{{\rho — {\rho _в}}}\]
По условию \(\rho = 3 \rho_в\), поэтому:
\[\frac{{{x_1}}}{{{x_2}}} = \frac{{3{\rho _в}}}{{3{\rho _в} — {\rho _в}}} = 1,5\]
Ответ: 1,5.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
3.3.40 Человек прыгает в воду со скалы высотой 10 м. На какую глубину он опустится
3.3.42 В цилиндрическом сосуде диаметром 50 см плавает льдинка объемом 12 дм3. В льдинку
3.3.43 Однородный конус массой 48 кг плавает в воде вершиной вниз. Определить высоту

 icodepro.ru
icodepro.ru