icodepro.ruУсловие задачи:
Стержень длиной \(l\) и массой \(m\) одним концом упирается в вертикальную стенку, а другой его конец удерживается нитью, длина которой равна длине стержня. При каком угле \(\alpha\) стержень будет находиться в равновесии, если коэффициент трения между стержнем и стеной равен 0,3?
Задача №3.1.25 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(l\), \(m\), \(\mu=0,3\), \(\alpha-?\)
Решение задачи:
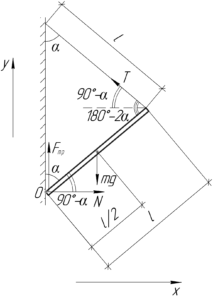Покажем на схеме все силы, которые действуют на стержень: это сила тяжести стержня \(mg\), сила натяжения нити \(T\) и компоненты реакции опоры в точке O – сила нормальной реакции \(N\) и сила трения \(F_{тр}\). Стержень находится в равновесии, поэтому мы можем записать первое условие равновесия в проекции на оси \(x\) и \(y\) (первый закон Ньютона) и второе условие равновесия относительно точки O (правило моментов). Все необходимые для определения проекций и плеч сил углы показаны на схеме.
\[\left\{ \begin{gathered}
{F_{тр}} + T \cdot \sin \left( {90^\circ – \alpha } \right) – mg = 0 \hfill \\
T \cdot \cos \left( {90^\circ – \alpha } \right) = N \hfill \\
mg \cdot \frac{l}{2} \cdot \cos \left( {90^\circ – \alpha } \right) – T \cdot l \cdot \sin \left( {180^\circ – 2\alpha } \right) = 0 \hfill \\
\end{gathered} \right.\]
Из тригонометрии известно, что \(\cos \alpha = \sin \left( {90^\circ – \alpha } \right)\), \(\sin \alpha = \cos \left( {90^\circ – \alpha } \right)\) и \(\sin 2\alpha = \sin \left( {180^\circ – 2\alpha } \right)\), поэтому:
\[\left\{ \begin{gathered}
{F_{тр}} + T \cdot \cos \alpha – mg = 0 \;\;\;\;(1)\hfill \\
T \cdot \sin \alpha = N \;\;\;\;(2)\hfill \\
mg \cdot \frac{l}{2} \cdot \sin \alpha – T \cdot l \cdot \sin 2\alpha = 0 \;\;\;\;(3)\hfill \\
\end{gathered} \right.\]
Поработаем над равенством (3). Так как \(\sin 2\alpha = 2\sin \alpha \cdot \cos \alpha\), то:
\[mg \cdot \frac{l}{2} \cdot \sin \alpha – T \cdot l \cdot 2\sin \alpha \cdot \cos \alpha = 0\]
\[\frac{{mg}}{2} – 2T \cdot \cos \alpha = 0\]
\[mg = 4T \cdot \cos \alpha \;\;\;\;(4)\]
Преобразуем равенство (2) в такой вид:
\[T = \frac{N}{{\sin \alpha }}\;\;\;\;(5)\]
Из равенства (1) выразим силу трения \(F_{тр}\):
\[{F_{тр}} = mg – T \cdot \cos \alpha \]
Учитывая ранее полученное равенство (4), имеем:
\[{F_{тр}} = 4T \cdot \cos \alpha – T \cdot \cos \alpha = 3T \cdot \cos \alpha \]
Так как \(T = \frac{N}{{\sin \alpha }}\) (формула (5)), то:
\[{F_{тр}} = \frac{{3N}}{{\sin \alpha }} \cdot \cos \alpha = \frac{{3N}}{{tg\alpha }}\]
Стержень будет оставаться в равновесии, пока имеет место сила трения покоя, т.е. справедливо неравенство:
\[{F_{тр}} \leq \mu N\]
Значит:
\[\frac{{3N}}{{tg\alpha }} \leq \mu N\]
\[\frac{3}{{tg\alpha }} \leq \mu \]
Произведем математические преобразования:
\[\frac{1}{{tg\alpha }} \leq \frac{\mu }{3}\]
\[tg\alpha \geq \frac{3}{\mu }\]
\[\alpha \geq arctg\left( {\frac{3}{\mu }} \right)\]
Минимальное значение угла \(\alpha\), при котором возможно равновесие, равно:
\[{\alpha _{\min }} = arctg\left( {\frac{3}{\mu }} \right)\]
\[{\alpha _{\min }} = arctg\left( {\frac{3}{{0,3}}} \right) = 84,3^\circ = 1,47\;рад\]
Ответ: 1,47 рад.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
3.1.24 Лестница составляет с землей угол 70 градусов и опирается о вертикальную гладкую
3.1.26 К вертикальной гладкой стене подвешен на тросе AB однородный шар массы M
3.1.27 К вертикальной гладкой стене подвешен на тросе AB однородный шар массы M. Определите
Ошибка в четвертой формуле. Должно быть mg=4T*2cosA, т.к. все множители должны домножиться на 2, а не только первый. Или я не прав?
Не правы.\[\frac{{mg}}{2} – 2T \cdot \cos \alpha = 0\]\[\frac{{mg}}{2} = 2T \cdot \cos \alpha \]\[mg = 4T \cdot \cos \alpha \]
А если стержень подвязан в центре и имеет длину в два раза меньше, чем у нити. Каким будет решение? Заранее спасибо
В следующий раз, пожалуйста, приводите полное условие задачи. Рисунок прикрепить в комментарии возможности не имею, но он практически такой же, как в решении, приведенном сверху (ну разве что стержень подвешен за середину). Угол между стержнем и стеной обозначу за \(\alpha\), а между нитью и стеной – \(\beta\). Запишем два условия равновесия (аналогично как в решении выше):\[\left\{ \begin{gathered}
T\sin \beta = N \hfill \\
T\cos \beta + {F_{тр}} = mg \hfill \\
T\sin \left( {\alpha + \beta } \right) \cdot \frac{l}{4} = mg\sin \alpha \cdot \frac{l}{4} \hfill \\
\end{gathered} \right.\]
Тогда:\[\left\{ \begin{gathered}
T\sin \beta = N \hfill \\
{F_{тр}} = mg – T\cos \beta \hfill \\
\frac{{T\sin \left( {\alpha + \beta } \right)}}{{\sin \alpha }} = mg \hfill \\
\end{gathered} \right.\]
Стержень будет оставаться в равновесии, пока имеет место сила трения покоя, т.е. справедливо неравенство:
\[{F_{тр}} \leq \mu N\]Поэтому:\[\frac{{T\sin \left( {\alpha + \beta } \right)}}{{\sin \alpha }} – T\cos \beta \leq \mu T\sin \beta \]\[T\sin \left( {\alpha + \beta } \right) – T\sin \alpha \cos \beta \leq \mu T\sin \alpha \sin \beta \]\[\sin \left( {\alpha + \beta } \right) – \sin \alpha \cos \beta \leq \mu \sin \alpha \sin \beta \]\[\sin \alpha \cos \beta + \cos \alpha \sin \beta – \sin \alpha \cos \beta \leq \mu \sin \alpha \sin \beta \]\[\cos \alpha \sin \beta \leq \mu \sin \alpha \sin \beta \]\[\cos \alpha \leq \mu \sin \alpha \]\[tg\alpha \geq \frac{1}{\mu }\]\[\alpha \geq arctg\left( {\frac{1}{\mu }} \right)\]Ну вот как-то так решается эта задача.
Добрый день. Подскажите, пожалуйста: можно ли выделить T из формулы 4?
А что значит “выделить”? Выразить? Конечно можно выразить, пожалуйста:\[T = \frac{{mg}}{{4\cos \alpha }}\]
Если остановиться на Fтр=3T*cos(а). Не использовать формулу 5. И написать а мин при Fтр=мю*N. То приравняв правые части и поставив формулу 2 получим T*sin(a) =3T*cos(a) и далее тангенс и арктангенс без значительной части Ваших преобразований. А так спасибо за решение.
Как я понял, Вы предлагаете так:\[3T\cos \alpha \leq \mu N\]Так как \(N = T\sin \alpha \), то:\[3T\cos \alpha \leq \mu T\sin \alpha \]\[3\cos \alpha \leq \mu \sin \alpha \]\[tg\alpha \geq \frac{3}{\mu }\]\[\alpha \geq arctg\left( {\frac{3}{\mu }} \right)\]Да, так решение чуть короче и менее запутано. Спасибо за комментарий, решение я поправлю в скором времени!
Почему в условии равновесия используется l*sin(180-2a), если этого не хватает, чтобы достать до линии действия силы?
Разложите вектор \(T\) на два таких вектора:
1) первый вектор – в направлении, перпендикулярном стержню, его модуль будет равен \(T \cdot \sin \left( {180 – 2\alpha } \right)\), плечо относительно точки O равно \(l\);
1) второй вектор – в направлении вдоль стержня, его модуль будет равен \(T \cdot \cos \left( {180 – 2\alpha } \right)\), плечо относительно точки O равно 0.
Так Вы и получите, что момент силы \(T\) относительно точки O равен \(T \cdot l \cdot \sin \left( {180 – 2\alpha } \right)\).
Какое плечо получилось у Вас?
Возможно я просто глупый, но почему мы раскладываем вектор Т по (180-2а), если у нас нет прямого угла для этого? Было бы справедливо при разложении на (90-а), там прямоугольный треугольник. А как в этом случае происходит разложение в непрямоугольном треугольнике – непонятно. Если хватит терпения выдержать мою недалёкость, то прошу объяснить.
Если мы разложим вектор T в направлении, совпадающим со стержнем, и в направлении, перпендикулярным стержню, то мы получим прямоугольный векторный треугольник.
Вообще, это неклассический способ нахождения момента силы. Если Вы все равно не понимаете, то делайте, как учат в школе – опускайте перпендикуляр из точки О на линию действия силы. В любом случае Вы получите такое же выражение для нахождения момента силы.
А почему в данной задаче сила реакции опоры направлена по нормали,а не под каким-то углом?
Потому что я эту силу реакции разложил на два вектора – F_тр и N.
То есть силу реакции можно либо представлять в виде одного вектора, направленного под каким-то углом, либо раскладывать на два взаимно перпендикулярных вектора (что я и сделал).
почему сила трения направлена вверх?
Стержень (точнее его нижний конец) стремится соскользнуть вниз, сила трения препятствует этому движению, поэтому она направлена наверх.
Зачем умножать на синус двух альфа?
В тексте решения есть пояснение, читайте внимательно. Также хорошенько изучите рисунок