В цилиндрическом сосуде диаметром 50 см плавает льдинка объемом 12 дм3. В льдинку

Условие задачи:

В цилиндрическом сосуде диаметром 50 см плавает льдинка объемом 12 дм³. В льдинку вмерз стальной шарик объемом 50 см³. На сколько изменится уровень воды в сосуде, если лед растает?

Задача №3.3.42 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(D=50\) см, \(V=12\) дм³, \(V_1=50\) см³, \(\Delta h-?\)

Решение задачи:

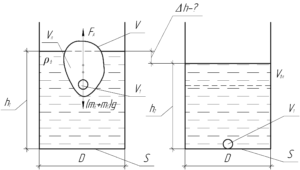Искомую величину \(\Delta h\) можно найти как разность высот конечного и начального уровня воды:

\[\Delta h = {h_2} – {h_1}\]

Всем известно, что тело, погруженное в жидкость, вытесняет объем воды, равный объему погруженной части тела. Поэтому начальную высоту жидкости в сосуде \(h_1\) можно найти по формуле:

\[{h_1} = \frac{{{V_в} + {V_п}}}{S}\]

Здесь \(V_в\) – объем изначально находившейся в сосуде воды, \(V_п\) – объем погруженной части льдинки, \(S\) – площадь поперечного сечения сосуда. Запишем аналогичную формулу для конечной высоты жидкости в сосуде \(h_2\):

\[{h_2} = \frac{{{V_в} + {V_{вл}} + {V_1}}}{S}\]

Здесь \(V_{вл}\) – объем воды, возникший из растаявшей льдинки. Тогда:

\[\Delta h = \frac{{{V_в} + {V_{вл}} + {V_1}}}{S} – \frac{{{V_в} + {V_п}}}{S}\]

\[\Delta h  = \frac{1}{S}\left( {{V_{вл}} + {V_1} – {V_п}} \right)\;\;\;\;(1)\]

Заметим, что масса растаявшего льда равна массе образовавшейся при этом воды. Поэтому чтобы определить объем воды \(V_{вл}\), запишем следующее равенство:

\[{m_л} = {m_в}\]

\[{\rho _л}\left( {V – {V_1}} \right) = {\rho _в}{V_{вл}}\]

\[{V_{вл}} = \frac{{{\rho _л}}}{{{\rho _в}}}\left( {V – {V_1}} \right)\;\;\;\;(2)\]

Для нахождения объема погруженной части льдинки \(V_п\) запишем условие плавания тел:

\[{F_А} = \left( {{m_л} + {m_1}} \right)g\]

Здесь \(m_л\) – масса льдинки, \(m_1\) – масса шарика. Распишем силу Архимеда и массы:

\[{\rho _в}g{V_п} = \left( {{\rho _л}\left( {V – {V_1}} \right) + {\rho _{ст}}{V_1}} \right)g\]

\[{V_п} = \frac{{{\rho _л}}}{{{\rho _в}}}\left( {V – {V_1}} \right) + \frac{{{\rho _{ст}}}}{{{\rho _в}}}{V_1}\;\;\;\;(3)\]

Подставим выражения (2) и (3) в формулу (1):

\[\Delta h = \frac{1}{S}\left( {\frac{{{\rho _л}}}{{{\rho _в}}}\left( {V – {V_1}} \right) + {V_1} – \frac{{{\rho _л}}}{{{\rho _в}}}\left( {V – {V_1}} \right) – \frac{{{\rho _{ст}}}}{{{\rho _в}}}{V_1}} \right)\]

\[\Delta h = \frac{1}{S}\left( {{V_1} – \frac{{{\rho _{ст}}}}{{{\rho _в}}}{V_1}} \right)\]

\[\Delta h = \frac{{{V_1}}}{S}\left( {1 – \frac{{{\rho _{ст}}}}{{{\rho _в}}}} \right)\]

Площадь основания цилиндрического сосуда найдем по формуле площади окружности:

\[S = \frac{{\pi {D^2}}}{4}\]

В итоге имеем:

\[\Delta h = \frac{{4{V_1}}}{{\pi {D^2}}}\left( {1 – \frac{{{\rho _{ст}}}}{{{\rho _в}}}} \right)\]

Переведем диаметр основания \(D\), объем \(V_1\) в систему СИ:

\[50\;см = 0,5\;м\]

\[50\;см^3 = 50 \cdot {10^{ – 6}}\;м^3\]

Плотность стали \(\rho_{ст}\) равна 7800 кг/м³, плотность воды \(\rho_{в}\) равна 1000 кг/м³. Считаем ответ:

\[\Delta h = \frac{{4 \cdot 50 \cdot {{10}^{ – 6}}}}{{3,14 \cdot {{0,5}^2}}}\left( {1 – \frac{{7800}}{{1000}}} \right) =  – 1,73 \cdot {10^{ – 3}}\;м =  – 1,73\;мм\]

Знак “минус” показывает, что уровень воды в сосуде уменьшится.

Ответ: уменьшится на 1,73 мм.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

3.3.41 Шарик подвесили на упругой пружине и опустили в воду. Во сколько раз уменьшилось
3.3.43 Однородный конус массой 48 кг плавает в воде вершиной вниз. Определить высоту
3.3.44 Цилиндр плавает в вертикальном положении в сосуде с водой. В сосуд подливают более