Условие задачи:
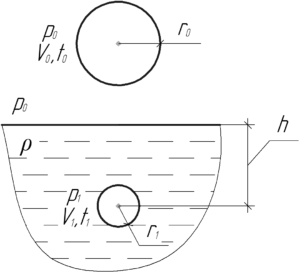
Тонкий резиновый шар радиусом 2 см наполнен воздухом при температуре 20° C и давлении 100 кПа. Каким будет радиус шара, если его опустить в воду с температурой 4° C на глубину 20 м?
Задача №4.2.89 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(r_0=2\) см, \(t_0=20^\circ\) C, \(p_0=100\) кПа, \(t_1=4^\circ\) C, \(h=20\) м, \(r_1-?\)
Решение задачи:
 Запишем объединённый газовый закон (уравнение Клапейрона) для воздуха, находящегося в шаре:
Запишем объединённый газовый закон (уравнение Клапейрона) для воздуха, находящегося в шаре:
\[\frac{{{p_0}{V_0}}}{{{T_0}}} = \frac{{{p_1}{V_1}}}{{{T_1}}}\;\;\;\;(1)\]
Поскольку резиновый шар легко деформируется, то давление воздуха внутри него всегда равно внешнему давлению. Поэтому изначально воздух в шаре оказывал давление, равное атмосферному \(p_0\). Затем, после погружения на глубину \(h\), давление воздуха в шаре станет равным давлению воды, которое определяется законом Паскаля:
\[{p_1} = {p_0} + \rho gh\]
Здесь \(\rho\) — плотность воды, равная 1000 кг/м3.
Объем шара в общем случае можно найти через его радиус \(r\) по формуле:
\[V = \frac{4}{3}\pi {r^3}\]
Тогда уравнение (1) примет вид:
\[\frac{{{p_0} \cdot \frac{4}{3}\pi r_0^3}}{{{T_0}}} = \frac{{\left( {{p_0} + \rho gh} \right) \cdot \frac{4}{3}\pi r_1^3}}{{{T_1}}}\]
Выразим из этого равенства искомый радиус \(r_1\):
\[\frac{{{p_0}r_0^3}}{{{T_0}}} = \frac{{\left( {{p_0} + \rho gh} \right)r_1^3}}{{{T_1}}}\]
\[r_1^3 = \frac{{{p_0}r_0^3{T_1}}}{{\left( {{p_0} + \rho gh} \right){T_0}}}\]
\[{r_1} = {r_0}\sqrt[3]{{\frac{{{p_0}{T_1}}}{{\left( {{p_0} + \rho gh} \right){T_0}}}}}\]
Переведем величины в систему СИ:
\[2\;см = 0,02\;м\]
\[20^\circ\;С = 293\;К\]
\[4^\circ\;С = 277\;К\]
Посчитаем ответ:
\[{r_1} = 0,02 \cdot \sqrt[3]{{\frac{{100 \cdot {{10}^3} \cdot 277}}{{\left( {100 \cdot {{10}^3} + {{10}^3} \cdot 10 \cdot 20} \right) \cdot 293}}}} = 0,014\;м\]
Ответ: 0,014 м.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
4.2.88 Внутри закрытого с обоих концов горизонтального цилиндра есть поршень
4.2.90 Цилиндрический сосуд делится невесомым поршнем на две части. В одну часть сосуда
4.2.91 Два одинаковых шара соединены тонкой трубкой, в которой находится капелька ртути

 icodepro.ru
icodepro.ru
Здравствуйте. Как рассчитать потраченную энергию при уменьшении объема газа?
ДЛЯ уменьшения объёма газа. Например, сколько потратится энергии при нажатии на поршень для уменьшения объёма цилиндра на 10%?
Не понимаю, как такое возможно, что давление в шаре, погружённом в воду будет больше, чем у шара, при атмосферной давлении?
Точнее, я не понимаю, почему давления стало равным Рo +pgh, а не просто pgh?
Давление внутри шара всегда равно полному давлению снаружи шара (ниже я объяснил почему).
Возьмите крайний случай, когда \(h \to 0\). По Вашей формуле получается, что давление шара, погруженного в воду близи её поверхности, равно нулю. При этом если шар вынуть из воды, то там давление воздуха там уже атмосферное. Нестыковка получается, из-за чего падение давления происходит?
Из-за того, что материал, из которого изготовлен шар (резина), легко деформируется, то давление внутри шара всегда равно давлению снаружи шара.
Но если бы шар был из стали (сталь плохо деформируется, точнее говоря, для деформации нужно гораздо большее давление), то давление уже было бы разным. Собственно говоря, поэтому мы и можем хранить газы под высоким давлением в газовых баллонах.
Перепутали местами 277 и 293. Написано в формуле одно, а подставляете наоборот. А так очень хорошо описан процесс решения, спасибо
Верно подметили, спасибо за дельное замечание и комплимент
Добрый вечер! Почему мы в данной задаче не выражаем плотность воды из уравнения Менделеева-Клапейрона?
Уравнение Клапейрона-Менделеева — это газовый закон, его нельзя использовать для веществ в жидком состоянии (тем более плотность воды — величина табличная).
Если Ваш вопрос был про уравнение (1) в моем решении, то могу сказать, что его можно вывести, дважды записав уравнение Клапейрона-Менделеева. Отмечу, что это уравнение (1) записано для воздуха в шаре.