Условие задачи:
Три равных по величине и знаку заряда \(q\) расположены в вакууме вдоль одной прямой на одинаковых расстояниях \(L\) друг от друга. Найти модуль напряженности электрического поля, созданного этими зарядами, в точке, находящейся на той же прямой посередине между двумя зарядами.
Задача №6.2.52 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(q\), \(L\), \(r=\frac{L}{2}\), \(E-?\)
Решение задачи:
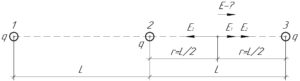 Искомая напряженность поля \(E\) в точке A равна геометрической (то есть векторной) сумме напряженностей полей от каждого из зарядов в этой точке. На схеме видно, что:
Искомая напряженность поля \(E\) в точке A равна геометрической (то есть векторной) сумме напряженностей полей от каждого из зарядов в этой точке. На схеме видно, что:
\[E = {E_1} + {E_2} — {E_3}\]
Распишем каждую из напряженностей \(E_1\), \(E_2\) и \(E_3\) по известной формуле, тогда получим:
\[E = \frac{{kq}}{{{{\left( {L + r} \right)}^2}}} + \frac{{kq}}{{{r^2}}} — \frac{{kq}}{{{r^2}}}\]
\[E = \frac{{kq}}{{{{\left( {L + r} \right)}^2}}}\]
Так как по условию задачи \(r=\frac{L}{2}\), то:
\[E = \frac{{kq}}{{{{\left( {L + \frac{L}{2}} \right)}^2}}} = \frac{{4kq}}{{9{L^2}}}\]
Коэффициент пропорциональности \(k\) и электрическая постоянная \(\varepsilon_0\) связаны формулой:
\[k = \frac{1}{{4\pi {\varepsilon _0}}}\]
Поэтому окончательно получим:
\[E = \frac{{4q}}{{9{L^2}}} \cdot \frac{1}{{4\pi {\varepsilon _0}}}\]
\[E = \frac{q}{{9\pi {\varepsilon _0}{L^2}}}\]
Ответ: \(\frac{q}{{9\pi {\varepsilon _0}{L^2}}}\).
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
6.2.51 Электрон, обладающий скоростью 18 км/с, влетает в однородное электрическое поле
6.2.53 Указать направление вектора напряженности электрического поля, созданного в точке
6.2.54 Точечный положительный заряд создаёт на расстоянии 10 см электрическое поле

 icodepro.ru
icodepro.ru
почему второй заряд имеет такую напряженность?
Если Вы откроете любой учебник по физике, то в одном из его параграфов будет сказано: «Напряженность поля E точечного положительного заряда q на расстоянии r равна k*q/r^2».