Условие задачи:
В сеть с напряжением 24 В включены два последовательно соединенных резистора. При этом сила тока 0,6 А. Когда резисторы подключили параллельно, сила тока стала 3,2 А. Определить большее из двух сопротивлений.
Задача №7.2.22 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(U=24\) В, \(I_1=0,6\) А, \(I_2=3,2\) А, \(R_A-?\)
Решение задачи:
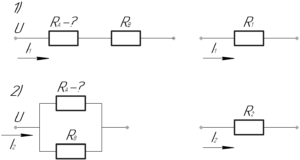 Эквивалентное сопротивление двух последовательно соединенных резисторов \(R_1\) в первом случае и двух параллельно соединенных резисторов \(R_2\) во втором случае равно:
Эквивалентное сопротивление двух последовательно соединенных резисторов \(R_1\) в первом случае и двух параллельно соединенных резисторов \(R_2\) во втором случае равно:
\[\left\{ \begin{gathered}
{R_1} = {R_A} + {R_B} \hfill \\
{R_2} = \frac{{{R_A} \cdot {R_B}}}{{{R_A} + {R_B}}} \hfill \\
\end{gathered} \right.\]
Запишем закон Ома для первого и второго случая:
\[\left\{ \begin{gathered}
{I_1} = \frac{U}{{{R_1}}} \hfill \\
{I_2} = \frac{U}{{{R_2}}} \hfill \\
\end{gathered} \right.\]
Учитывая первую систему, имеем:
\[\left\{ \begin{gathered}
{I_1} = \frac{U}{{{R_A} + {R_B}}} \hfill \\
{I_2} = \frac{{U\left( {{R_A} + {R_B}} \right)}}{{{R_A} \cdot {R_B}}} \hfill \\
\end{gathered} \right.\]
\[\left\{ \begin{gathered}
U = {I_1}\left( {{R_A} + {R_B}} \right) \hfill \;\;\;\;(1)\\
U = {I_2}\frac{{{R_A} \cdot {R_B}}}{{{R_A} + {R_B}}} \hfill \\
\end{gathered} \right.\]
Тогда имеем такое равенство:
\[{I_1}\left( {{R_A} + {R_B}} \right) = {I_2}\frac{{{R_A} \cdot {R_B}}}{{{R_A} + {R_B}}}\]
\[{I_1}{\left( {{R_A} + {R_B}} \right)^2} = {I_2}{R_A}{R_B}\]
В левой части раскроем квадрат суммы и правую часть перенесем в левую:
\[{I_1}R_A^2 + 2{I_1}{R_A}{R_B} + {I_1}R_B^2 — {I_2}{R_A}{R_B} = 0\]
\[{I_1}R_A^2 + \left( {2{I_1} — {I_2}} \right){R_A}{R_B} + {I_1}R_B^2 = 0\]
Разделим обе части на \(R_B^2\), тогда:
\[{I_1}{\left( {\frac{{{R_A}}}{{{R_B}}}} \right)^2} + \left( {2{I_1} — {I_2}} \right)\frac{{{R_A}}}{{{R_B}}} + {I_1} = 0\]
Решим это квадратное уравнение относительно \(\frac{R_A}{R_B}\) (учтите, раз мы приняли, что большим сопротивлением обладает резистор A, то это отношение должно быть больше 1).
Посчитаем дискриминант:
\[D = {\left( {2{I_1} — {I_2}} \right)^2} — 4I_1^2\]
\[\frac{{{R_A}}}{{{R_B}}} = \frac{{{I_2} — 2{I_1} \pm \sqrt {{{\left( {2{I_1} — {I_2}} \right)}^2} — 4I_1^2} }}{{2{I_1}}}\]
\[\left[ \begin{gathered}
\frac{{{R_A}}}{{{R_B}}} = \frac{{{I_2} — 2{I_1} + \sqrt {{{\left( {2{I_1} — {I_2}} \right)}^2} — 4I_1^2} }}{{2{I_1}}} \hfill \\
\frac{{{R_A}}}{{{R_B}}} = \frac{{{I_2} — 2{I_1} — \sqrt {{{\left( {2{I_1} — {I_2}} \right)}^2} — 4I_1^2} }}{{2{I_1}}} \hfill \\
\end{gathered} \right.\]
Посчитаем численные значения:
\[\left[ \begin{gathered}
\frac{{{R_A}}}{{{R_B}}} = \frac{{3,2 — 2 \cdot 0,6 + \sqrt {{{\left( {2 \cdot 0,6 — 3,2} \right)}^2} — 4 \cdot {{0,6}^2}} }}{{2 \cdot 0,6}} \hfill \\
\frac{{{R_A}}}{{{R_B}}} = \frac{{3,2 — 2 \cdot 0,6 — \sqrt {{{\left( {2 \cdot 0,6 — 3,2} \right)}^2} — 4 \cdot {{0,6}^2}} }}{{2 \cdot 0,6}} \hfill \\
\end{gathered} \right.\]
\[\left[ \begin{gathered}
\frac{{{R_A}}}{{{R_B}}} = 3 \hfill \\
\frac{{{R_A}}}{{{R_B}}} = \frac{1}{3} \hfill \\
\end{gathered} \right.\]
Как было уже сказано выше, должно выполняться условие \(\frac{{{R_A}}}{{{R_B}}} > 1\), поэтому второй корень нам не подходит. Значит:
\[\frac{{{R_A}}}{{{R_B}}} = 3\]
Чтобы найти сопротивление \(R_A\), воспользуемся (1):
\[U = {I_1}\left( {{R_A} + {R_B}} \right)\]
Так как мы получили, что \({R_B} = \frac{{{R_A}}}{3}\), то:
\[U = {I_1}\left( {{R_A} + \frac{{{R_A}}}{3}} \right)\]
\[U = \frac{{4{I_1}{R_A}}}{3}\]
Откуда:
\[{R_A} = \frac{{3U}}{{4{I_1}}}\]
Посчитаем ответ:
\[{R_A} = \frac{{3 \cdot 24}}{{4 \cdot 0,6}} = 30\;Ом = 0,03\;кОм\]
Ответ: 0,03 кОм.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
7.2.21 Батарея гальванических элементов с ЭДС 15 В и внутренним сопротивлением 5 Ом замкнута
7.2.23 Щелочной аккумулятор создает силу тока 0,8 А, если его замкнуть на сопротивление 1,5 Ом
7.2.24 Какова ЭДС источника, если при измерении напряжения на его зажимах вольтметром

 icodepro.ru
icodepro.ru