Условие задачи:

В центре закрепленной полусферы радиуса $R$, заряженной равномерно с поверхностной плотностью зарядов $+ \sigma$, в вакууме расположен маленький шарик, заряженный зарядом $+q$. Если шарик освободить, то в процессе движения он приобретет максимальную кинетическую энергию. Найти кинетическую энергию.

Задача №6.3.62 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

$R$, $+ \sigma$, $+q$, $W_к-?$

Решение задачи:

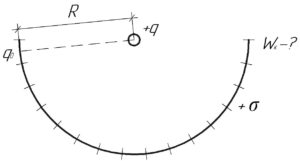Понятно, что для решения этой задачи следует воспользоваться законом сохранения энергии, согласно которому потенциальная энергия взаимодействия $W_п$ заряда шарика $q$ с зарядами на полусфере перейдёт (на бесконечности) в кинетическую энергию шарика $W_к$.

$${W_к} = {W_п}\;\;\;\;(1)$$

Получается нам, чтобы найти ответ на вопрос задачи, необходимо всего лишь найти потенциальную энергию взаимодействия $W_п$ заряда шарика $q$ с зарядами на полусфере. Для этого выполним следующий «трюк» — выделим на полусфере очень маленький участок (практически точечный, смотрите на рисунке поперечное сечение полусферы), который несёт некоторый малый заряд $q_0$. Потенциальную энергию взаимодействия $W_0$ заряда $q_0$ с зарядом $q$, находящимся на расстоянии $R$ от него, можно определить по такой формуле:

$${W_0} = \frac{{kq{q_0}}}{R}\;\;\;\;(2)$$

Понятно, что полную энергию $W_п$ можно найти как сумму всех энергий $W_0$:

$${W_п} = \sum {{W_0}}$$

Учитывая (2), получим:

$${W_п} = \sum {\frac{{kq{q_0}}}{R}}$$

$${W_п} = \frac{{kq}}{R}\sum {{q_0}} \;\;\;\;(3)$$

Понятно, что выражение $\sum {{q_0}}$ определяет суммарный заряд на полусфере, который, очевидно, можно найти как произведение поверхностной плотности заряда $\sigma$ на площадь полусферы $S$.

$$\sum {{q_0}} = \sigma S$$

Тогда (3) примет такой вид:

$${W_п} = \frac{{kq\sigma S}}{R}\;\;\;\;(4)$$

Площадь полусферы $S$ можно найти через её радиус $R$ по такой формуле (половина площади сферы):

$$S = 2\pi {R^2}\;\;\;\;(5)$$

Также выразим коэффициент пропорциональности $k$ через электрическую постоянную $\varepsilon _0$:

$$k = \frac{1}{{4\pi {\varepsilon _0}}}\;\;\;\;(6)$$

Подставим (5) и (6) в (4):

$${W_п} = \frac{1}{{4\pi {\varepsilon _0}}} \cdot \frac{{q\sigma }}{R} \cdot 2\pi {R^2}$$

$${W_п} = \frac{{\sigma qR}}{{2{\varepsilon _0}}}$$

Принимая во внимание формулу (1), окончательно имеем:

$${W_к} = \frac{{\sigma qR}}{{2{\varepsilon _0}}}$$

Ответ: $\frac{{\sigma qR}}{{2{\varepsilon _0}}}$.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

6.3.61 Какую работу необходимо совершить, чтобы три одинаковых точечных положительных
6.3.63 В центре закрепленной полусферы радиуса R, заряженной равномерно
6.3.64 На тонком закрепленном кольце радиуса R равномерно распределен заряд q. Какова