Условие задачи:

Велосипедист начал свое движение из состояния покоя и в течение первых 4 с двигался с ускорением 1 м/с², затем в течение 0,1 мин он двигался равномерно, и последние 20 м — равнозамедленно до остановки. Найти среднюю скорость за все время движения.

Задача №1.3.42 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(t_1=4\) с, \(a_1=1\) м/с², \(t_2=0,1\) мин, \(S_3=20\) м, \(\upsilon_{ср}-?\)

Решение задачи:

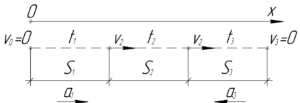Понятно, что в этой задаче мы имеем дело с тремя участками пути \(S_1, S_2, S_3\), которые велосипедист будет проезжать за время \(t_1, t_2, t_3\) соответственно. Поэтому среднюю скорость \(\upsilon_{ср}\) на всем пути можно найти по формуле:

\[{\upsilon _{ср}} = \frac{{{S_1} + {S_2} + {S_3}}}{{{t_1} + {t_2} + {t_3}}}\]

Начнем с самого первого участка. Велосипедист здесь двигался равноускоренно с ускорением \(a_1\) без начальной скорости в течение \(t_1\) секунд. Пройденный им путь \(S_1\) легко найти из формулы:

\[{S_1} = \frac{{{a_1}t_1^2}}{2}\]

Найдем также скорость \(\upsilon_2\) на конце первого участка, поскольку именно с этой скоростью человек будет двигаться равномерно весь второй участок.

\[{\upsilon _2} = {a_1}{t_1}\]

Теперь разберемся со вторым участком пути. Как уже было сказано, он будет пройден равномерно со скоростью \(\upsilon_2\). Определим длину пути \(S_2\) из простой формулы:

\[{S_2} = {\upsilon _2}{t_2}\]

Используя ранее выведенную формулу, имеем:

\[{S_2} = {a_1}{t_1}{t_2}\]

Ну и наконец, последний третий участок. Его человек на велосипеде будет проезжать равнозамедленно, очевидно имея скорость в начале участка, равную \(\upsilon_2\). Запишем следующую формулу:

\[\upsilon _3^2 — \upsilon _2^2 =  — 2{a_3}{S_3}\]

Скорость в конце всего пути \(\upsilon_3\), очевидно, равна нулю, поэтому:

\[\upsilon _2^2 = 2{a_3}{S_3} \Rightarrow {a_3} = \frac{{\upsilon _2^2}}{{2{S_3}}}\]

Формула скорости для равнозамедленного движения:

\[\upsilon  = {\upsilon _0} — at\]

Применительно к нашему случаю:

\[0 = {\upsilon _2} — {a_3}{t_3} \Rightarrow {t_3} = \frac{{{\upsilon _2}}}{{{a_3}}} = \frac{{{\upsilon _2} \cdot 2{S_3}}}{{\upsilon _2^2}} = \frac{{2{S_3}}}{{{\upsilon _2}}} = \frac{{2{S_3}}}{{{a_1}{t_1}}}\]

В итоге, окончательная формула для нахождения средней скорости на всем пути такая:

\[{\upsilon _{ср}} = \frac{{\frac{{{a_1}t_1^2}}{2} + {a_1}{t_1}{t_2} + {S_3}}}{{{t_1} + {t_2} + \frac{{2{S_3}}}{{{a_1}{t_1}}}}}\]

Переведем 0,1 мин в систему СИ:

\[0,1\; мин = 0,1 \cdot 60\; с = 6\; с\]

Заменим величины в формуле численными данными задачи и рассчитаем ответ.

\[{\upsilon _{ср}} = \frac{{\frac{{1 \cdot {4^2}}}{2} + 1 \cdot 4 \cdot 6 + 20}}{{4 + 6 + \frac{{2 \cdot 20}}{{1 \cdot 4}}}} = 2,6\; м/с = 9,36\; км/ч\]

Ответ: 9,36 км/ч.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

1.3.41 Частица, начав двигаться из состояния покоя и пройдя некоторый путь
1.3.43 Два велосипедиста едут навстречу: один из них, имея скорость 7,2 км/ч, спускается
1.3.44 За первую секунду равноускоренного движения тело проходит путь равный 1 м