Условие задачи:
Велосипедист начинает двигаться делать поворот по кругу со скоростью 10 м/с, а заканчивает со скоростью 5 м/с. Определите максимальное отношение центростремительных ускорений во время поворота.
Задача №1.8.16 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\upsilon_1=10\) м/с, \(\upsilon_2=5\) м/с, \(\frac{a_{ц1}}{a_{ц2}}-?\)
Решение задачи:
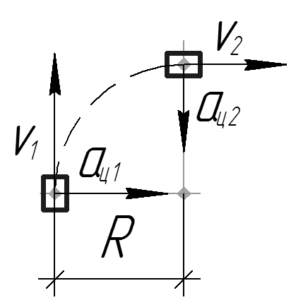 Центростремительное ускорение можно всегда найти, зная скорость \(\upsilon\) и радиус кривизны траектории \(R\), по следующей формуле:
Центростремительное ускорение можно всегда найти, зная скорость \(\upsilon\) и радиус кривизны траектории \(R\), по следующей формуле:
\[a_ц = \frac{{{\upsilon ^2}}}{R}\]
Видно, что центростремительное (или его ещё называют нормальным) ускорение прямо пропорционально квадрату скорости \(\upsilon\) и обратно пропорционально радиусу кривизны траектории \(R\). Значит, в начале центростремительное ускорение у велосипедиста было больше, нежели в конце, из-за более высокой скорости, поэтому нужно найти отношение \(\frac{a_{ц1}}{a_{ц2}}\), поскольку оно будет наибольшим. Радиус кривизны \(R\) в ходе движения не меняется.
\[\frac{{{a_{ц1}}}}{{{a_{ц2}}}} = \frac{{\upsilon _1^2 \cdot R}}{{R \cdot \upsilon _2^2}} = \frac{{\upsilon _1^2}}{{\upsilon _2^2}} = {\left( {\frac{{{\upsilon _1}}}{{{\upsilon _2}}}} \right)^2}\]
В итоге максимальное отношение центростремительных ускорений равно:
\[\frac{{{a_{ц1}}}}{{{a_{ц2}}}} = {\left( {\frac{{10}}{5}} \right)^2} = 4\]
Ответ: 4.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.8.15 К валу, радиус которого 5 см, прикреплена нить. Через 5 с после начала равномерного
1.8.17 Вертолет начал снижаться вертикально вниз с ускорением 0,2 м/с2. Лопасть винта
1.8.18 Вычислить путь, который проехал за 30 с велосипедист, двигающийся с угловой

 icodepro.ru
icodepro.ru
Не понять выражение
«Определите максимальное отношение… «