Условие задачи:
Машинист локомотива, движущегося со скоростью 72 км/ч, начал тормозить на расстоянии 1000 м от станции. Определить, через какое время локомотив остановится, если при торможении его ускорение 0,2 м/с2.
Задача №1.3.13 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\upsilon_0=72\) км/ч, \(S=1000\) м, \(a=0,2\) м/с2, \(t-?\)
Решение задачи:
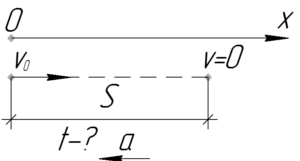 Самый простой путь решения этой задачи — это воспользоваться формулой скорости при равнозамедленном движении:
Самый простой путь решения этой задачи — это воспользоваться формулой скорости при равнозамедленном движении:
\[\upsilon = {\upsilon _0} — at\]
Так как спрашивается время \(t\), за которое локомотив остановится, значит, конечная скорость \(\upsilon\) состава равна нулю.
\[\upsilon = 0\]
Получается, чтобы найти время \(t\) необходимо решить линейное уравнение.
\[0 = {\upsilon _0} — at\]
\[t = \frac{{{\upsilon _0}}}{a}\]
Перед тем как подставлять значения величин, переведем начальную скорость \(\upsilon_0\) из км/ч в м/с.
\[72\; км/ч = \frac{{72 \cdot 1000}}{{1 \cdot 3600}}\; м/с = \frac{{720}}{{36}}\; м/с = 20\; м/с \]
Сосчитаем теперь искомое время.
\[t = \frac{{20}}{{0,2}} = 100\; с = 1\; мин\; 40\; с\]
Странно, но в условии даны лишние данные, например, путь \(S\). Давайте проверим, действительно ли локомотив пройдет до остановки такое расстояние, для этого воспользуемся уравнением пути для равнозамедленного движения:
\[S = {\upsilon _0}t — \frac{{a{t^2}}}{2}\]
\[S = 20 \cdot 100 — \frac{{0,2 \cdot {{100}^2}}}{2} = 1000\; м \]
Поскольку полученное значение совпадает с данным в условии, значит, мы решили задачу верно.
Ответ: 1 мин 40 с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.3.12 Вычислить тормозной путь автомобиля, имеющего начальную скорость 60 км/ч
1.3.14 Поезд, имеющий скорость 90 км/ч, стал двигаться с замедлением 0,3 м/с2. Найти
1.3.15 Пуля со скоростью 200 м/с ударяет в земляной вал и проникает в него на глубину

 icodepro.ru
icodepro.ru
по условию задачи тело тормозит…
Дано; V_1 = 72 км/час; V_2 = 0 м/с; a = — 0.2 м/с^2
0 = V_1 + (- 0.2)* t
и не надо мудрить…
Можно проще, через формулу ускорения. Там получится рабочая формула t=(v-v0)/a.
Да, так тоже правильно, но следует учитывать, что \({\upsilon _0} > \upsilon \), поэтому правильнее:\[t = \frac{{{\upsilon _0} — \upsilon }}{a}\]
Используя расстояние, можно через квадратное уравнение решить, приняв время за x или так и оставить t.
Можно, но решать квадратное уравнение сложнее, чем линейное
3600 откуда это число
Это количество секунд в одном часу