Условие задачи:

При падении камня в колодец его удар о поверхность воды доносится через 5 с с момента падения. Принимая скорость звука равной 330 м/с, определить глубину колодца.

Задача №1.4.42 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(t=5\) с, \(\upsilon_{зв}=330\) м/с, \(H-?\)

Решение задачи:

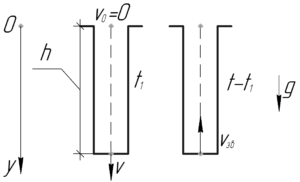И звук, и камень проходят одинаковое расстояние, равное глубине колодца \(H\), но первый движется равномерно, а второй равноускоренно без начальной скорости. Пусть камень падал \(t_1\) секунд, тогда звук достиг человека через \(\left( {t — {t_1}} \right)\), поэтому верно следующее:

\[\left\{ \begin{gathered}
H = \frac{{gt_1^2}}{2} \hfill \\
H = \upsilon_{зв} \left( {t — {t_1}} \right) \hfill \\
\end{gathered} \right.\]

Приравняв оба выражения и раскрыв скобки, получим следующее квадратное уравнение. Необходимо решить его.

\[\frac{{gt_1^2}}{2} = {\upsilon _{зв}}t — {\upsilon _{зв}}{t_1}\]

\[\frac{{gt_1^2}}{2} + {\upsilon _{зв}}{t_1} — {\upsilon _{зв}}t = 0\]

Подставим численные значения буквенных величин.

\[5t_1^2 + 330{t_1} — 1650 = 0\]

\[t_1^2 + 66{t_1} — 330 = 0\]

Сосчитаем дискриминант этого квадратного уравнения.

\[D = {66^2} + 4 \cdot 330 = 5676\]

\[{t_1} = \frac{{ — 66 \pm \sqrt {5676} }}{2}\]

\[\left[ \begin{gathered}
{t_1} = 4,67 \; с \hfill \\
{t_1} = — 70,67 \; с \hfill \\
\end{gathered} \right.\]

Естественно, что время падения не может выражаться отрицательным числом, поэтому не берем в расчет второй корень.

Чтобы найти глубину колодца \(H\), воспользуемся вторым выражением из приведенной выше системы.

\[H = 330\left( {5 — 4,67} \right) = 108,9 \; м \approx 0,1\; км \]

Ответ: 0,1 км.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

1.4.41 Парашютист сразу после прыжка пролетает расстояние 50 м с пренебрежимо
1.4.43 Свободно падающий камень пролетел последние три четверти пути за одну
1.4.44 Тело начинает свободно падать с высоты 45 м. В тот же момент с высоты 24 м