Условие задачи:
В сеть с напряжением 220 В включены последовательно десять ламп сопротивлением по 24 Ом и напряжением 12 В каждая. Лишнее напряжение поглощается реостатом. Определить сопротивление реостата.
Задача №7.2.14 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(U=220\) В, \(N=10\), \(R_0=24\) Ом, \(U_0=12\) В, \(R_1-?\)
Решение задачи:
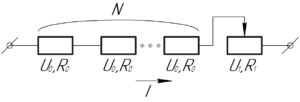 Согласно закону Ома для участка цепи сила тока на реостате \(I\) равна отношению напряжения на реостате \(U_1\) к его текущему сопротивлению \(R_1\):
Согласно закону Ома для участка цепи сила тока на реостате \(I\) равна отношению напряжения на реостате \(U_1\) к его текущему сопротивлению \(R_1\):
\[I = \frac{{{U_1}}}{{{R_1}}}\]
Поэтому сопротивление реостата \(R_1\) мы найдем по формуле:
\[{R_1} = \frac{{{U_1}}}{I}\;\;\;\;(1)\]
Так как все лампы и реостат соединены последовательно, то верно следующее равенство (напряжение сети равно сумме напряжений на лампах и реостате):
\[U = N{U_0} + {U_1}\]
Откуда имеем:
\[{U_1} = U — N{U_0}\;\;\;\;(2)\]
Опять же, так как лампы и реостат соединены последовательно, значит через них течет один и тот же ток \(I\), который, зная напряжение и сопротивление каждой лампы, можно определить по формуле:
\[I = \frac{{{U_0}}}{{{R_0}}}\;\;\;\;(3)\]
Подставим (2) и (3) в (1), тогда получим:
\[{R_1} = \frac{{\left( {U — N{U_0}} \right){R_0}}}{{{U_0}}}\]
Задача решена в общем виде, осталось только посчитать численный ответ:
\[{R_1} = \frac{{\left( {220 — 10 \cdot 12} \right) \cdot 24}}{{12}} = 200\;Ом = 0,2\;кОм\]
Ответ: 0,2 кОм.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
7.2.13 Определить силу тока в проводнике R1, если ЭДС источника 14 В, его внутреннее сопротивление
7.2.15 ЭДС источника 6 В. При внешнем сопротивлении цепи 1 Ом сила тока 3 А. Какой будет
7.2.16 Источник тока с внутренним сопротивлением 1,5 Ом замкнут на резистор 1,5 Ом. Когда в цепь

 icodepro.ru
icodepro.ru
Ошибка в дано «N=20». По суте должно быть не 20, а 10
Спасибо за замечание, исправил!