Условие задачи:
Вольтметр, внутреннее сопротивление которого равно 50 кОм, подключенный к источнику постоянного тока последовательно с дополнительным сопротивлением, равным 120 кОм, показывает напряжением 100 В. Определите напряжение на клеммах источника тока.
Задача №7.5.49 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(R_v=50\) кОм, \(R_{доп}=120\) кОм, \(U_0=100\) В, \(U-?\)
Решение задачи:
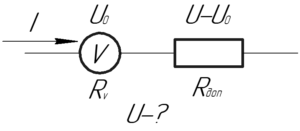 Так как вольтметр и дополнительное сопротивление соединены последовательно, то через них течет одинаковый ток \(I\). Напряжение на вольтметре согласно условию задачи равно \(U_0\), тогда на дополнительном сопротивлении напряжение будет равно \(\left( {U — {U_0}} \right)\), где \(U\) — искомое напряжение на зажимах источника. Запишем дважды закон Ома для участка цепи:
Так как вольтметр и дополнительное сопротивление соединены последовательно, то через них течет одинаковый ток \(I\). Напряжение на вольтметре согласно условию задачи равно \(U_0\), тогда на дополнительном сопротивлении напряжение будет равно \(\left( {U — {U_0}} \right)\), где \(U\) — искомое напряжение на зажимах источника. Запишем дважды закон Ома для участка цепи:
\[\left\{ \begin{gathered}
I = \frac{{{U_0}}}{{{R_v}}} \hfill \\
I = \frac{{U — {U_0}}}{{{R_{доп}}}} \hfill \\
\end{gathered} \right.\]
Тогда, очевидно, имеем:
\[\frac{{{U_0}}}{{{R_v}}} = \frac{{U — {U_0}}}{{{R_{доп}}}}\]
Тогда, перемножив «крест-накрест», получим:
\[{U_0}{R_{доп}} = U{R_v} — {U_0}{R_v}\]
\[{U_0}{R_{доп}} + {U_0}{R_v} = U{R_v}\]
\[{U_0}\left( {{R_{доп}} + {R_v}} \right) = U{R_v}\]
В итоге получим такую формулу для получения ответа на вопрос задачи:
\[U = \frac{{{U_0}\left( {{R_{доп}} + {R_v}} \right)}}{{{R_v}}}\]
Подставим численные данные задачи в эту формулу и посчитаем ответ:
\[U = \frac{{100 \cdot \left( {120 \cdot {{10}^3} + 50 \cdot {{10}^3}} \right)}}{{50 \cdot {{10}^3}}} = 340\;В\]
Ответ: 340 В.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
7.5.48 В схеме, изображенной на рисунке, R1=5 Ом, R2=6 Ом, R3=3 Ом, сопротивлением амперметра
7.5.50 Определите показание амперметра в электрической цепи, изображенной на рисунке
7.5.51 Какой величины надо взять дополнительное сопротивление, чтобы можно было включить

 icodepro.ru
icodepro.ru